Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.Problemas - Ex. 44
Calcule a função de rede e a resposta ao impulso, se a saída é .
Passo 1
Eu acredito é na rapaziada
Que segue em frente e segura o rojão
Eu ponho fé é na fé da moçada
Que não foge da fera e resolve a questão...
Com esse belo prólogo, vamos começar a resolução desta maravilhosa questão:
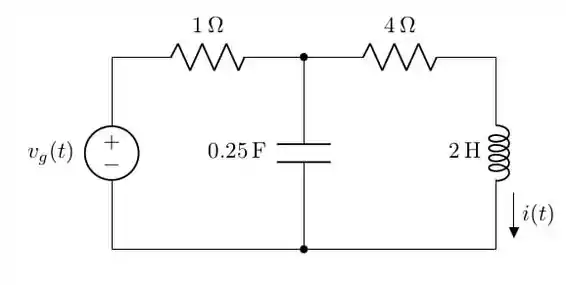
Como bem sabemos, o primeiro passo é transformar o circuito. Assim:
Assim, vamos calcular a função de transferência. Primeiramente, vamos usar o método das tensões de nó:
De posse da tensão no nó, podemos encontrar pela relação:
Passo 2
Uma vez que conhecemos a entrada e a saída no domínio da frequência, podemos encontrar a função de transferência:
Passo 3
Para encontrarmos a resposta ao impulso, vamos voltar com a função de rede para o domínio do tempo. Antes, vamos fazer uma modificação na função de transferência:
Assim, essa expressão “mamão com açúcar” é muito fácil de relacionar com sua função no domínio do tempo: