Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Introdução a Análise de Circuitos, de Boylestad- Ed: 10º - Capítulo 15.Problemas - Ex. 5

Calcule a impedância total dos circuitos mostrados na Figura 15.117. Expresse a resposta nas formas retangular e polar e construa o diagrama de impedâncias.

Passo 1

Fala galeraaa, vem comigo que no caminho eu explico!!

Encoxxta

  1. Consulte a fig 15.117 (a) no livro

    2. Escreva a equação e encontre a impedância resistiva na forma polar.

    Z R   ∠   0 ° = R Ω ∠ 0 °

    Converta a forma polar para retangular.

    Z R = R

    Considere a equação e encontre a impedância indutiva na forma polar.

    Z L = X L ∠ 90 °

    Converta a forma polar para a retangular.

    Z L = j   X L

    Considere a equação encontre a impedância capacitiva na forma polar.

    Z C = X C   ∠ - 90 °

    Converta a forma polar para a retangular.

    Z C = - j X C

    Passo 2

    Considere a equação e encontre a impedância total.

    Z T = Z R + Z L + Z C        

    Z T = R + j X L - j X C

    Substituindo

    Z T = 3 Ω + j 4 Ω - j 7 Ω

    Z T = 3 Ω - j 3 Ω

    Converta a forma retangular em polar

    Z T = 4.24   Ω   ∠ - 45 °

    Podemos ver que a forma polar da impedância total é 4.24   Ω   ∠ - 45 ° e a forma retangular da impedância total é 3 Ω - j 3 Ω .

    Passo 3

    Desenharemos o diagrama de impedância para o circuito fornecido.

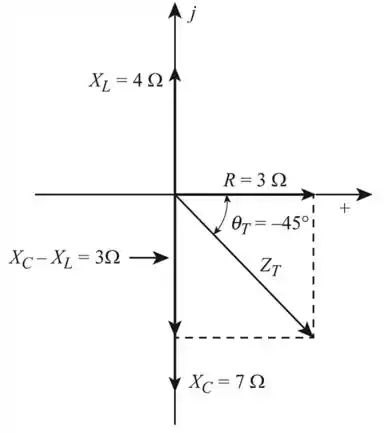
    Passo 4

  2. Consulte a fig 15.117 (b) no livro

    3. Escreveremos a equação e encontraremos a impedância total.

    Z T = R + j X L 1 + j X L 2 - j X C

    Vamos substituir os valores

    Z T = 0.5 × 10 3 Ω +   j 2 × 10 3 Ω +   j 5 × 10 3 Ω - (   j 4 × 10 3 Ω )

    Z T = 0.5 + j 2 + j 5 - j 4 k Ω

    Z T = 0.5 + j 3 k Ω

    Converta para a forma polar

    Z T = 3041.38 Ω ∠ 80.53 °

    Logo, a forma polar da impedância total é 3041.38 Ω ∠ 80.53 ° e a forma retangular da impedância total e de 0.5 + j 3 k Ω .

    Passo 5

    Vamos desenhar o diagrama de impedância para o circuito fornecido.

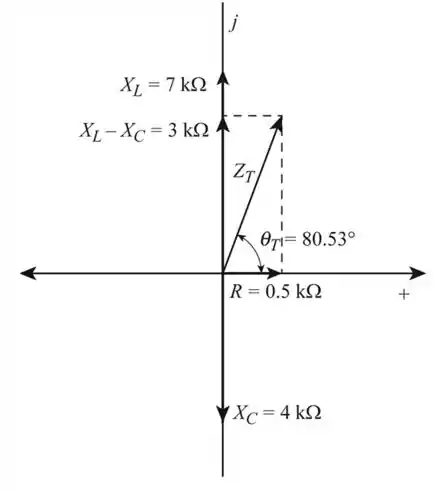
    Passo 6

  3. Consulte a figura 15.117 ( c ) no livro

Escreva a fórmula e encontre a reatância indutiva para L 1 .

X L 1 = ω L 1

Substituindo

X L 1 = 2 π f L 1

X L 1 = 2 π × 1 × 10 3 × 0.06

X L 1 = 0.376   k Ω

Considere a seguinte fórmula e encontre a reatância indutiva para L 2 .

X L 2 = ω L 2

Substituindo

X L 2 = 2 π f L 2

X L 2 = 2 π × 1 × 10 3 × 0.2

X L 2 = 1.256   k Ω

Considere a seguinte expressão e com ela encontraremos a reatância capacitiva para C

X C = 1 2 π f C

Substituindo

X C = 1 2 π 1 × 10 3 × 10 × 10 - 6

X C = 15.915   Ω

Passo 2

Consulte a fig 15.117 ( c ) no livro.

Escreva a equação e encontre a impedância total.

Z T = R + j X L 1 + j X L 2 - j X C

Substituindo

Z T = 47 Ω + j 0.376 × 10 3 Ω + j 1.256 × 10 3 Ω - j 15.915 Ω

Z T = 47 Ω + j 1616.085 Ω

Converta a formula retangular em polar

Z T = 1616.76 Ω ∠ 88.33 °

Logo, a forma polar da impedância total é 1616.76 Ω ∠ 88.33 ° e a forma retangular da impedância total é de   47 Ω + j 1616.085 Ω .

Passo 3

Desenhe o diagrama de impedância para o circuito fornecido.

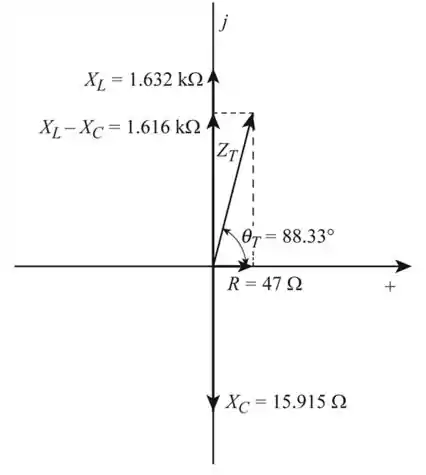
Resposta

Ei, a resposta está no passo a passo :)