Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.5 - Ex. 1
Calcule a potência complexa entregue a uma carga que tem um fator de potência de 0,85 (adiantado) e (a) absorve . (b) . e (c) .
Passo 1
Iae, meus queridos! Td certinho??
Esta questão é bem tranquilinha, ela nos deu o fator de potência de 0,85, e todos os dados de potência temos que dar um jeito de transformar para Potência Aparente (VA).
Para fazer essa transformação, vamos usar o triangulo de potências.
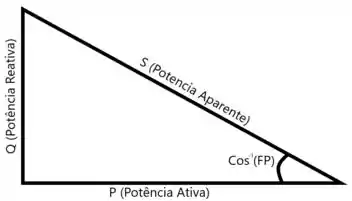
O fator de potência é o mesmo para todos os casos, então o ângulo é o mesmo para todos os casos, vamos calcula-lo!
OBS. A questão nos informou que o fator de potencia está adiantado, ou seja, esse ângulo que calculamos, deve ser negativo.
Passo 2
Na letra (a), a potência dada é de , ou seja, observando a unidade, vemos que se trata de um valor de potência ativa.
Usando o triangulo de potencias acima, temos que calcular a potência aparente.
Podemos realizar esse cálculo fazendo a razão entre a potência ativa e o cosseno do ângulo.
Portanto, sua notação complexa é
Passo 3
Na letra (b), a potência dada é de , ou seja, observando a unidade, vemos que se trata de um valor de potência reativa.
Usando o triangulo de potencias acima, temos que calcular a potência aparente.
Podemos realizar esse cálculo fazendo a razão entre a potência ativa e o seno do ângulo.
Portanto, sua notação complexa é
Passo 4
Na letra (c) é bem simples, ele já nos deu o valor da potência em VA, ou seja, em potência aparente, então sua notação complexa é
Resposta
(a)
(b)
(c)