Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.Problemas - Ex. 34

Calcule a potência máxima que pode ser entregue ao resistor de R no circuito do Prob. 5.12.

Passo 1

Falaaa, galerinha!!! Vamos mandar ver nessa questão 😉.

Dá uma olhadinha no circuito. Ele quer que achemos a potência máxima no resistor R e no problema 5.12 nos foi dito que R = 2 . Agora, que já sabemos o que a questão nos pede, vamos mandar ver!

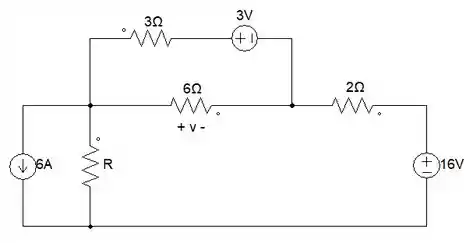
Vamos usar o mesmo principio de resolução do Prob. 5.12, a superposição, só que vamos achar a corrente que está passando em R . Vamos lá 💪

Pra começar, vamos resolver o circuito com apenas a fonte de 3V

Percebeu que a tensão de 3v está em paralelo com o resistor de 3 Ω ? Vamos fazer transformação de fonte!

i = V R 3

i = 3 3

i = 1 A

Belezinha! Agora, já podemos fazer a equivalência dos resistores ☺️.

Viu que o resistor de 3Ω agora ficou em paralelo com o resistor de 6Ω? Vamos fazer a associação deles.

R 3 // R 6 = 3 ⋅ 6 3 + 6

R 3 // R 6 = 18 9

R 3 // R 6 = 2 Ω

O resistor de 2   Ω   está série com o de 2   Ω .

R 2 - R 2 = 2 + 2

R 2 - R 2 = 4 Ω

Boa, pessoal! Com isso, o resistor de 4 Ω fica em paralelo com o de 2Ω e como temos uma fonte de corrente, vamos fazer divisor de corrente!

i 1 = R 2 R 2 + R 4 ⋅ i

i 1 = 2 2 + 4 ⋅ 1

i 1 = 0,33 A

Calma! Ainda não temos a corrente do resistor R , precisamos fazer mais uma divisão de corrente. Vamos lá!

i 2 = R 4 R 2 + R 2 ⋅ i 1

i 2 = 4 2 + 2 ⋅ 0,33

i 2 = 0,33 A

Agora, sim! Com o valor da corrente, podemos saber a potência🤩

P 1 = R ⋅ i 2 2

P 1 = 2 ⋅ 0,33 2

P 1 = 0,2178 W

Passo 2

Está indo muito bem! Vamos continuar assim! 🤩. Agora, vamos apenas a fonte de 16V. Vamos lá 💪

Viu que mais uma vez o resistor de 3Ω ficou em paralelo com o resistor de 6Ω? Vamos fazer a associação deles.

R 3 // R 6 = 3 ⋅ 6 3 + 6

R 3 // R 6 = 18 9

R 3 // R 6 = 2 Ω

O resistor de 2   Ω   está série com o de 2   Ω   e o outro de 2   Ω

R 2 - R 2 - R 2 = 2 + 2 + 2

R 2 - R 2 - R 2 = 6 Ω

Maravilha! Feito isso, temos um resistor de 6 Ω em série com a fonte de 16V. Vamos fazer LKT na malha?!

6 ⋅ i = 16

i = 16 6

i = 2,66 A

Agora, sim! Com o valor da corrente, podemos saber a potência🤩

P 2 = R ⋅ i 2

P 2 = 2 ⋅ 2,66 2

P 2 = 14,1512 W

Passo 3

Maravilha! Só está faltando acharmos a potência para quando tiver a fonte de 6A. Olha só como está nosso circuito até agora.

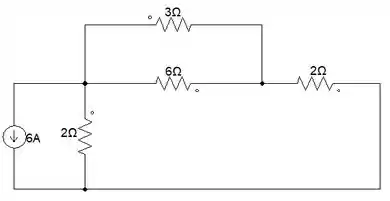
Viu que mais uma vez o resistor de 3Ω ficou em paralelo com o resistor de 6Ω? Vamos fazer a associação deles.

R 3 // R 6 = 3 ⋅ 6 3 + 6

R 3 // R 6 = 18 9

R 3 // R 6 = 2 Ω

O resistor de 2   Ω   está série com o de 2   Ω .

R 2 - R 2 = 2 + 2

R 2 - R 2 = 4 Ω

Com isso, nossos resistores de 4 Ω e 2 Ω ficarão em paralelo e como temos uma fonte de corrente podemos fazer divisor de corrente. Bora lá!

i 1 = R 4 R 2 + R 4 ⋅ i

i 1 = 4 2 + 4 ⋅ - 6

i 1 = - 4 A

Agora, sim! Com o valor da corrente, podemos saber a potência🤩

P 3 = R 2   ⋅ i 1 2

P 3 = 2   ⋅ ( - 6 ) 2

P 3 = 32 W

Passo 4

Estamos quase terminando. Só falta somarmos todas as potências encontradas e teremos a potência máxima fornecida pelo resistor R . 🤩

P m = P 1 + P 2 + P 3

P m = 0,2178 + 14,1512 + 32

P m = 46,369 W

Resposta

P m = 46,369 W