Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.2 - Ex. 1
Calcule a resposta forçada da Fig 11.3 usando a análise de malha
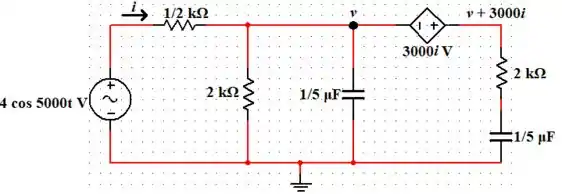
Passo 1
Opaa!! Seguinte... Vamos primeiro passar os valores da fonte para a forma polar enxergar o capacitor em forma de reatância.
Lembrando que:
Em que rad/s.
Logo, temos:
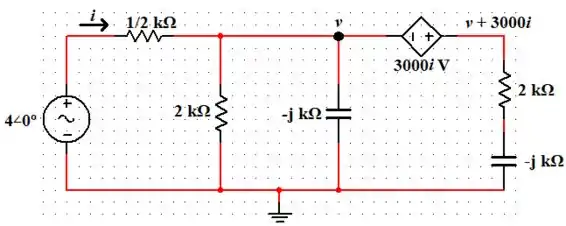
Passo 2
Agora, vamos redesenhar a análise de malha para prosseguirmos com a Lei de Kirchhoff das Tensões (LKT):
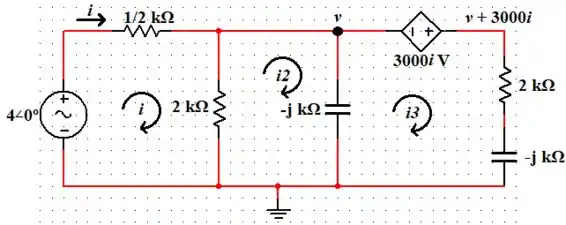
Passo 3
Dessa forma, utilizando a Lei dos Kirchhoff das Tensões na malha , temos:
Fazendo a meeesma coisa com a malha :
E também a mesma coisa na malha :
Passo 4
Assim, temos o seguinte sistema:
Resolvendo o sistema pela Regra de Cramer para o sistema 3x3, temos que é:
Portanto, temos:
Resposta
Exercícios de Livros Relacionados
O valor da corrente I 0 no capacitor da Figura 10.44 é: 4 ∠ 0 °A b) 2.4 ∠ - 90 °A c) 0.6 ∠ 0 ° Ad) - 1A
Determine i no circuito da Figura 10.50.
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Determine V o no circuito da Figura 10.52.
Calcule v o ( t ) no circuito da Figura 10.53.