Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 38

10.38. Calcule a resposta forçada i. [Sugestão: Note que I = V/Z não funciona, visto que Z(j 1) = 0. Resolva a equação representativa pelo método da Seç. 9.6.].

Passo 1

Eai galerinha, tudo beleza?

Vamos para mais um exercício show de bola?!

Primeiramente, vamos montar a nova cara do circuito da nossa questão:

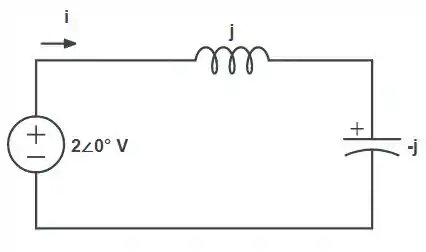
Vamos resolver este exercício, utilizando a excitação na frequência natural.

Sabendo que:

i = d V d t

d i d t + V = 2 cos ⁡ t

V + d 2 i d t 2 = 2 cos ⁡ t

Em resposta natural, temos:

λ 2 + 1 = 0

λ = j

Na resposta em frequência, temos:

V = t ( A cos ⁡ t + B   s e n   t )

d V = A cos ⁡ t + B   s e n   t + t   ( - A   s e n   t + B   c o s   t )

d 2 V = - A   s e n   t + B cos ⁡ t - A   s e n   t + B cos ⁡ t + t ( - A cos ⁡ t - B   s e n   t )

V + d 2 V d t 2 = - 2   A   s e n   t + 2   B cos ⁡ t = 2 cos ⁡ t

- 2   A = 2 → A =   - 1 2   B = 0 → B = 0

Daí, temos:

V f = - t   c o s   t

E, portanto:

i f = ( -   c o s   t + t   s e n   t )   A

Resposta

i f = ( -   c o s   t + t   s e n   t )   A