Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.Problemas - Ex. 45

Calcule a resposta i ( t ) no Prob. 18.44, se o circuito está inicialmente em repouso e v g t = u t - u t - 1   V .

Passo 1

Simbora, galera! Bora resolver essa questão que é tipo uma continuação da questão anterior. Vamos usar boa parte do que vimos lá, mas fique tranquilo que o que for necessário, vamos repetir aqui:

Vamos começar desenhando o circuito em questão:

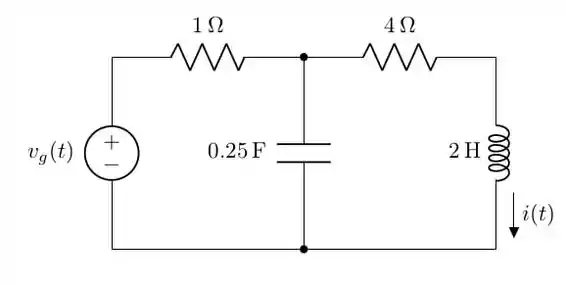
E para este circuito, vamos precisar do circuito transformado:

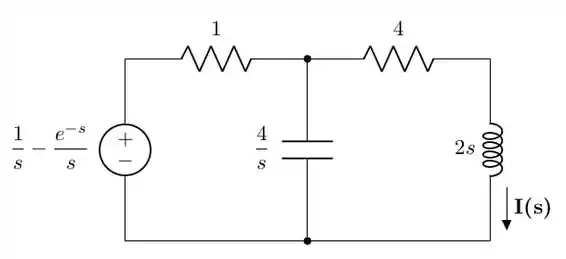
Passo 2

Antes de usar o circuito transformado, vamos poupar tempo usando o que fizemos na questão 18.44:

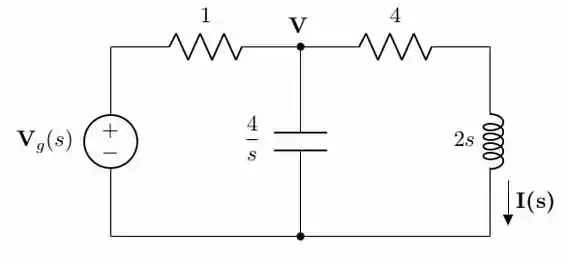
A análise de circuito para o circuito acima foi a seguinte:

V - V g 1 + V 4 / s + V 2 s + 4 = 0

⇒ V - V g + s ⋅ V 4 + V 2 s + 4 = 0

⇒ 8 s + 2 V - 8 s + 2 V g + 2 s s + 2 V + 4 V = 0

⇒ 8 s + 16 + 2 s 2 + 4 s + 4 V - 8 s + 2 V g = 0

⇒ V = 8 s + 2 V g 2 s 2 + 12 s + 20 = 4 s + 2 V g s 2 + 6 s + 10

De posse da tensão no nó, podemos encontrar I ( s ) pela relação:

I = V 2 s + 4 = 2 2 s + 4 V g ( 2 s + 4 ) ( s 2 + 6 s + 10 ) = 2 V g s 2 + 6 s + 10

No nosso caso, usando a expressão para v g ( t ) , teremos:

I = 2 s 2 + 6 s + 10 ⋅ 1 - e - s s = 2 s s 2 + 6 s + 10 - 2 ⋅ e - s s s 2 + 6 s + 10 = I 1 - I 2

Este artifício que vamos usar de separar I em 2 frações será muito útil lá na frente quando iremos poupar muito trabalho braçal.

Passo 3

Vamos começar separando I 1 em frações parciais:

I 1 =   2 s s 2 + 6 s + 10 = A s + B s + C s 2 + 6 s + 10

A =   s I 1 s = 0 = 2 s 2 + 6 s + 10 s = 0 = 2 10 ⇒ A = 1 5

Trabalhando apenas com os numeradores, iremos obter:

2 = 1 5 s 2 + 6 s + 10 + B s 2 + C s ⇒ B + 1 5 s 2 + 6 5 + C s + 2 = 2

Essa equação nos leva aos seguintes resultados:

B = - 1 5     e   C = - 6 5

Assim, vamos obter a seguinte expressão para I 1 :

I 1 = 2 s - 1 5 s + 6 ( s 2 + 6 s + 10 ) = 2 s - 1 5 s + 6 ( s 2 + 6 s + 9 + 1 ) = 2 s - 1 5 s + 6 s + 3 2 + 1

= 2 s - 1 5 s + 3 + 3 s + 3 2 + 1 = 2 s - 1 5   s + 3 s + 3 2 + 1 + 3 ⋅ 1 s + 3 2 + 1

Logo,

i 1 t = 1 5 - 1 5 ⋅ e - 3 t cos ⁡ t + 3 sin ⁡ t u ( t )

Passo 4

Agora aqui entra o “pulo do gato”. Ao invés de fazermos uma nova bateria de frações parciais para I 2 , vamos usar a “simetria” que existe entre as frações para encontrar uma expressão semelhante para I 2 .

Assim, temos:

i 2 t = 1 5 - 1 5 e - 3 t - 1 cos ⁡ t - 1 + 3 sin ⁡ t - 1 u ( t - 1 )

Como a resposta final é uma combinação das duas correntes, temos então que:

i t = i 1 t - i 2 t = 1 5 - 1 5 ⋅ e - 3 t cos ⁡ t + 3 sin ⁡ t u t - 1 5 - 1 5 e - 3 t - 1 cos ⁡ t - 1 + 3 sin ⁡ t - 1 u ( t - 1 )  

Resposta

i t = 1 5 - 1 5 ⋅ e - 3 t cos ⁡ t + 3 sin ⁡ t u t - 1 5 - 1 5 e - 3 t - 1 cos ⁡ t - 1 + 3 sin ⁡ t - 1 u ( t - 1 )