Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 19

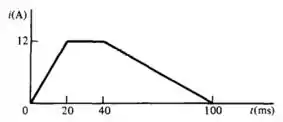
Calcule a tensão sobre um indutor de 10-mH em t = 10 ms, 30 ms e 60 ms. se a corrente é como a indicada na figura

Passo 1

Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para achar a tensão em um indutor através de um gráfico de corrente. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??

Nosso primeiro passo vai ser analisar os trechos do gráfico, considerando a equação da reta. Podemos escrever como:

i ( t )   =   3 5 t   ,                                       0 < t < 20

i ( t )   =   12   ,                                     20 < t < 40

i ( t )   = - 1 5 t + 20   ,           40 < t < 100

Passo 2

Ok, agora o nosso problema vai ser relembrar qual a fórmula da relação entre a corrente e a tensão em um indutor. Responde Aí!! Lembrou?? Não?!

Nos foi fornecida a forma de onda da corrente em função do tempo para o nosso indutor. Sendo assim, podemos perceber que a nossa corrente vai ser dada por intervalos e devemos nos lembrar ainda que a tensão em um indutor é dada por:

v = L ∙ d i d t

Onde L é a constante de proporcionalidade que chamamos de indutância do indutor.

Passo 3

Agora vamos para o último passo!!

Em t =   10 m s

v = L ∙ d i d t   =   10 ⋅ 1 0 - 3 d (   3 5 t ) d t   =   6   m V

Em t =   30 m s

v = L ∙ d i d t   =   10 ⋅ 1 0 - 3 d (   12 ) d t   =   0   V

Em t =   60 m s

v = L ∙ d i d t   =   10 ⋅ 1 0 - 3 d (   - 1 5 t + 20 ) d t   =   - 2   m V

Pronto!!

Resposta

Em t =   10   m s

v =   6   m V

Em t =   30   m s

v =   0   V

Em t =   60   m s

v =   - 2   m V

Exercícios de Livros Relacionados

Um indutor de 2-mH tem uma tensão v = 2 cos 1000 t V com i(0) = 1,5 A. Calcule a energia armazenada no indutor em t = π/6 ms
Na Fig. 7.10, seja I = 5 A, R1 = 6𝝮, R2 = 4 𝝮, L = 2H, e i1(0-) = 2 A. Se a chave é aberta em t = O-, encontre iL(0-), iL(0+), i1(0+) e diL(0+)/dt.
Calcule os valores máximo e mínimo da indutância que pode ser obtida usando-se 10 indutores de 10-mH.
Deduza uma equação para a divisão de corrente entre dois indutores em paralelo, sem corrente inicial, por meio de i1 e i2.
Calcule a indutância equivalente. (Os valores dos indutores são dados em mH.)