Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.Problemas - Ex. 41
Calcule , para , usando o circuito transformado, se e .
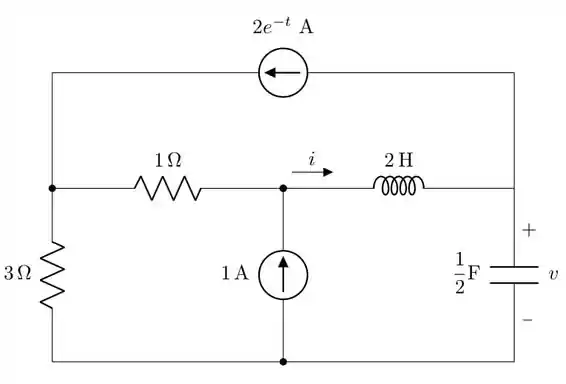
Passo 1
Fala, galerinha do bem! Vamos resolver esse circuitinho aqui começando por transformar o circuito no domínio do tempo para o domínio da frequência:
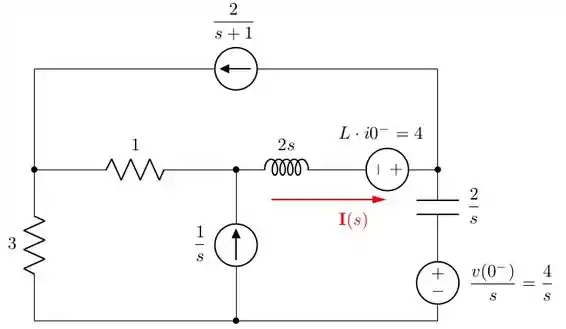
Na figura, colocamos as condições iniciais pelas fontes de tensão em série com o indutor e capacitor, respeitando a polaridade para cada elemento. Sendo assim, vamos começar a nossa análise.
Passo 2
A gente pode tanto usar o método das tensões de nó ou o das correntes de malha. Vamos escolher as correntes de malha porque temos 2 fontes de corrente e isso nos fornece 2 supermalhas. Isso facilita bastante as contas:
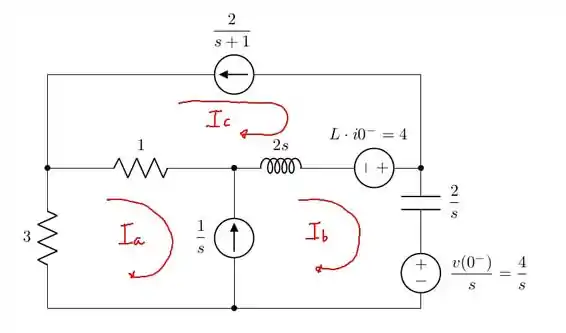
Assim, as duas equações de supernó que temos são:
e
Para encontrarmos a terceira equação, vamos “esquecer” as fontes de corrente que contribuíram para o supernó e vamos analisar o que sobra. Assim, obtemos:
Substituindo as duas equações de supernó na equação anterior, vamos encontrar que
Passo 3
Não nos foi solicitado as correntes fictícias, mas sim a corrente que passa pelo indutor. No domínio da frequência, essa corrente foi representada pela cor vermelha na figura 2. Assim, comparando as figuras 2 e 3, podemos perceber que
E o que temos que fazer agora é separar esta expressão dada em frações parciais:
Assim, a expressão para é
Passo 4
Para encontrarmos a resposta no domínio do tempo, vamos utilizar uma relação que não usamos com frequência neste capítulo, e é a seguinte:
Assim, a corrente no domínio do tempo será dada por: