Para o circuito da figura 12.88:
a) Encontre as expressões matemáticas para a tensão e a corrente após a chave ser fechada
b) Esboce as formas de onda de e obtidas no item (a)
c) Determine uma expressão matemática para a tensão após a chave ser fechada e esboce a forma de onda correspondente
Passo 1
Oláááá galera, vamos lá resolver esse exercício
a) Para seguirmos com o que o exercício pede, vamos encontrar o equivalente de Thevenin nos terminais do circuito abaixo, pra aí encontrarmos as informações que precisamos
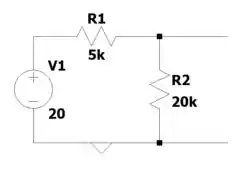
Temos
E a tensão de Thevenin:
Por fim, a indutância equivalente é
Passo 2
Agora, para encontrarmos as expressões de e de , precisamos também calcular o :
Agora sim, vamos encontrar , ele vai ser dado por
Substituindo os valores:
Passo 3
Agora vamos encontrar . Ele vai ser dado por
Substituindo os valores:
Fechouuuu
Passo 4
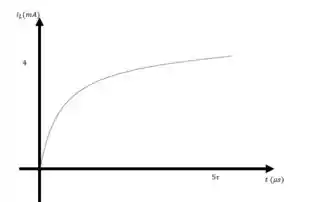
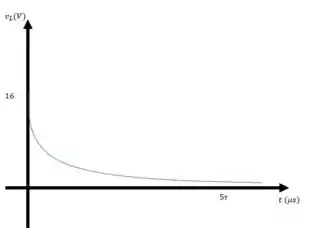
b) Vamos lá plotar os gráficos
Sabemos que
Analisando algebricamente, quando , temos e
Quando , temos e
Então os gráficos ficam assim
Passo 5
c) Vamos olhar só pra parte direita do circuito, ali do lado direito de onde está escrito :
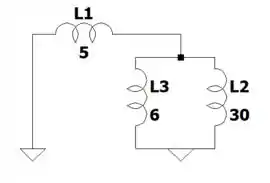
Quando escrevemos isso em termos da indutância equivalente (que calculamos no passo 1), vai ficar
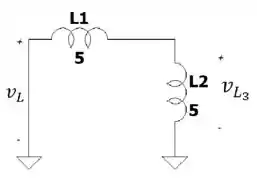
Basicamente: a tensão é a que “passa” pelos dois indutores, e a é a que passa só pelo segundo indutor
Como os dois indutores têm o mesmo valor, então devemos ter a mesma queda de tensão nos dois
Logo:
Substituindo a expressão de :
Passo 6
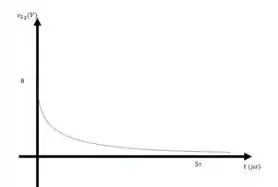
Vamos esboçar o gráfico de
Quando , temos
Quando , temos
Então:
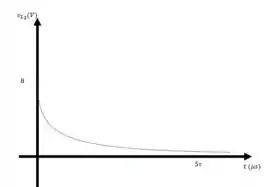
Acabouuu (:
Resposta
a)
b) 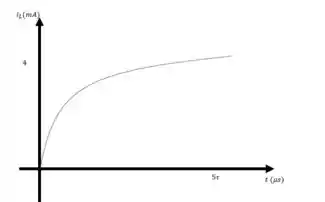
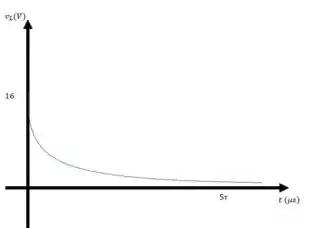
c)