Para o circuito da figura 12.71:
a) Escreva as expressões matemáticas para a corrente e a tensão após a chave ser fechada. Preste atenção no valor e no sentido da corrente inicial.
b) Esboce as formas de onda de e para o período entre o instante em que a chave é fechada e aquele em que o circuito atinge o estado estacionário
Passo 1
Nesse exercício, vamos trabalhar com esse circuito:
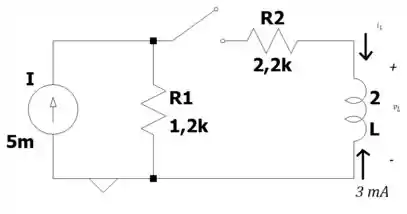
Bora lá analisar esse circuito :D
a) Para encontrarmos as expressões de e , precisamos encontrar , que é dado por
Substituindo os valores de e :
Então
Passo 2
Antes de qualquer coisa, podemos fazer a conversão da fonte de corrente em paralelo com o resistor para uma fonte de tensão em série com o resistor, onde
Então:
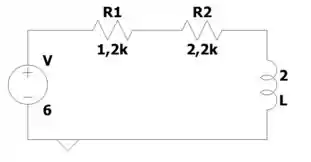
Somando os resistores:
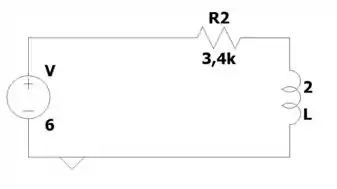
Agora vamos lá!
Passo 3
Quando a chave é fechada, a expressão de é dada por
Onde
Então:
Fechou?
Passo 4
Agora vamos encontrar a expressão de
Podemos fazer a Lei de Kirchoff das Tensões:
Onde é a tensão no resistor, que vale
Substituindo:
Então a expressão de é:
E é isso aíí
Passo 5
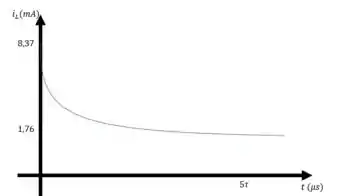
b) Vamos lá plotar os gráficos. Temos
Quando , . Quando , tende a
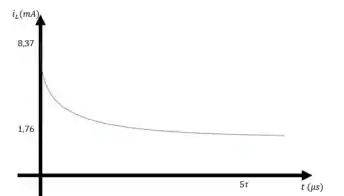
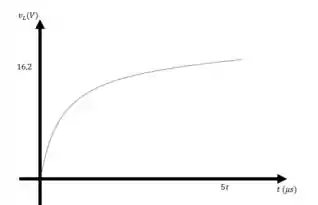
Para , temos
Quando , temos . Quando , temos
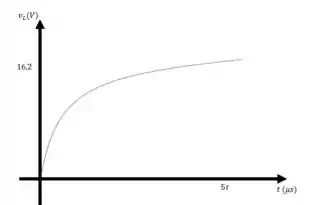
E acabaaaamosss
Resposta
a)
b)