Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 30
Para o circuito mostrado, e . Se a entrada e a saida forem e , respectivamente, calcule a funçāo de rede e esboce as respostas em amplitude e fase. Mostre que o pico da amplitude e a fase zero ocorrem em .
Passo 1
E aí gurizada tudo belezinha? O enunciado pede que a gente calcule a função de rede e esboce as respostas em amplitude e fase. Mostre que o pico da amplitude e a fase zero ocorrem em .
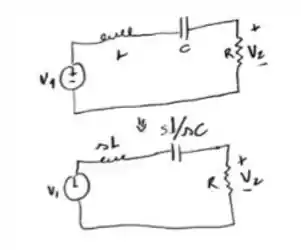
Depois do esboço do circuito partiu calcular 😊
Para amplitude máxima
Resposta
Exercícios de Livros Relacionados
Calcule a resposta completa v para t0 , usando a funçāo de rede, se v 0 * e d v 0 + / d t sāo iguais a zero
Mostre que, para a Fig. 14.16, em função dos parâmetros de transmissão, temos V 2 V 1 = 1 A + B Confira o resultado, usando essa fórmula para a rede com o resistor do Prob. 14.32
Execute as operações indicadas a seguir para formas de onda não-senoidais:a. 60 + 70 s e n ω t + 20 s e n 2 ω t + 90 ∘ + 10 s e n 3 ω t + 60 ∘ + [ 20 + 30 s e n ω t - 20 c o s 2 ω t + 5 c o
Determine a corrente i s no circuito visto na Figura 25.37 . i 2 = 10 + 30 s e n 20 t - 0,5 s e n 40 t + 90 ∘ i 1 = 20 + 4 s e n 20 t + 90 ∘ + 0,5 s e n 40 t + 30 ∘
A expansão em série de Fourier da tensão na entrada do circuito visto na Figura 25.33 é: e = 18 + 30 sen 400 t a. Obtenha a expressão da corrente i .b. Calcule o valor rms da corrente.c. Obtenha uma e