Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 1
Para o circuito mostrado, , e . Se a entrada e a saída forem e , respectivamente, calcule a função de rede e esboce as respostas em amplitude e fase. Mostre que o pico de amplitude e a fase zero ocorrem em rad/s.
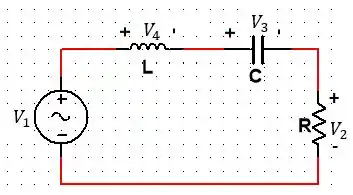
Passo 1
Eaeeeee, beleza?? Eita que parece complicado ein?
Mas calma!!!
Sabemos que, para uma resistência , a impedância é:
Para uma indutância , sua impedância é:
E, para uma capacitância , sua impedância é:
Assim, temos o seguinte circuito:
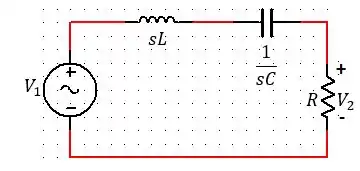
Passo 2
Fazendo o divisor de tensão para descobrir , temos:
Substituindo pelos valores de , e , temos:
Passo 3
Sabendo que :
Assim, o módulo da função de rede é dado por:
Logo, para a amplitude máxima, temos: