Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.Problemas - Ex. 29
No circuito do Prob. 5.16, calcule a potência entregue ao resistor de 4Ω através do uso de transformações sucessivas de fontes para obter o equivalente de Thévenin de tudo, exceto o resistor de 4Ω.
Passo 1
Falaaa, galerinha!!!
Vamos mandar ver nessa questão 😉. Dá uma olhadinha no circuito. Ele quer que achemos a potência do resistor de 4Ω e faça equivalente de Thévenin menos do resistor de 4Ω então mantê-lo intacto. Agora, que já sabemos o que a questão nos pede, vamos mandar bronca!
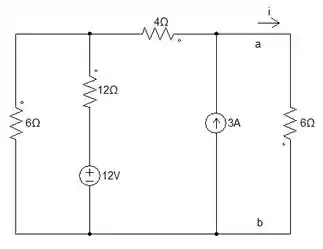
Antes de tudo, precisamos saber o nosso e para isso, precisamos desligar todas as fontes deixando apenas os resistores, lembrando que o resistor de 4 Ω será mantido intacto. Então, vamos lá 💪
Assim ficará nosso circuito apenas com os resistores necessários e sem as fontes.
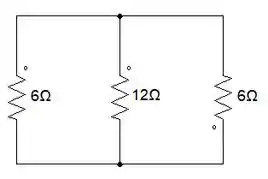
O resistor de 6Ω está em paralelo com o de 12Ω.
//
//
//
O resistor de está em série com o de .
= 6 + 4
= 10Ω
Então 10Ω
Passo 2
Muito bem, pessoal! Tá tirando onda, vamos continuar assim! Feito isso, agora vamos descobrir a tensão que está passando no resistor de 4Ω e no resistor de 6Ω.
Assim ficará nosso circuito agora:
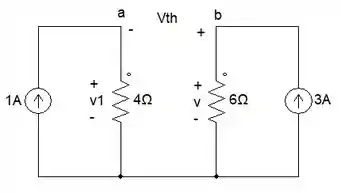
Olha só, ficou faltando apenas sabermos o valor da tensão , vamos fazer LKT e achamos rapidinho 😉.
Passo 3
Show de bola!!! Estamos quase terminando. 😍 Olha aí como vai ficar nosso circuito agora:
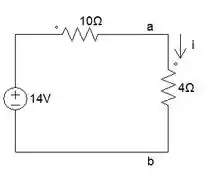
Bonitão né? Uma dica: só precisa achar agora a corrente que está passando em 4Ω. Assim fica fácil dms né não?? Vamos lá!
Aí simmm! Agora, podemos saber a potência no resistor de 4Ω.
Resposta
10Ω