Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 3.Problemas - Ex. 30

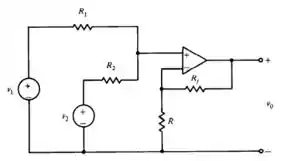
Se Rf = R1 = 1 k Ω no circuito do Prob. 3.29, calcule os valores dos demais resistores de forma que Vo = V1 + V2. (Note que o resultado é verdadeiro se R = Rf = R1 = R2.)

Passo 1

Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para o determinar os valores dos resistores. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??

Passo 2

Então bora láa!!

Utilizando a fórmula dado pelo exercício 4.29, temos que

v 0 =   ( 1 + R f R ) ( R 2 v 1 +   R 1 v 2 R 1 +   R 2 )

Substituindo os valore dados no enunciado

v 0 =   1 + 1 R ( R 2 v 1 +   1 v 2 1 +   R 2 )

E que v 0 =   v 1 + v 2

v 1 + v 2 =   1 + 1 R ( R 2 v 1 +   1 v 2 1 +   R 2 )

Passo 3

Agora vamos para o último passo!!

Vamos simplificar essa equação gigante com operações algébricas

v 1 + v 2 =   ( 1 + 1 R ) ( R 2 v 1 +   1 v 2 1 +   R 2 )

v 1 + v 2 =   ( R + 1 R ) ( R 2 v 1 +   v 2 1 +   R 2 )

v 1 + v 2 =   R + 1 R ( R 2 v 1 1 +   R 2 + v 2 1 +   R 2 )

Vamos supor que R   =   R 2 =   1   Ω

Então

v 1 + v 2 =   ( 2 ) ( v 1 +   v 2 2 )

v 1 + v 2 =   v 1 + v 2

Verdadeiro!!

Portanto

R   =   R 2 =   1   Ω

Pronto!!

Resposta

R   =   R 2 =   1   Ω