Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 9
Considere um circuito sem fontes que tem uma resposta . Mostre que uma linha reta que é tangente ao gráfico desta resposta no tempo intercepta o eixo de tempo (abscissa) no tempo . (Note que a Fig. 8.7 é o caso .)
Passo 1
Iae, meus queridos!! Td blzinha??
Para provar o enunciado, podemos chutar qualquer valor para e . Por exemplo, vamos usar , e .
Nesse caso, , portanto:
A resposta fica...
Vamos plotar esse gráfico.
A linha verde, se trata de e a tracejada de .
Passo 2
Vamos derivar .
Também vamos relembrar a formula da reta tangente:
Vamos escolher primeiramente.
, e
Nesse instante,
Vamos plotar o gráfico com .
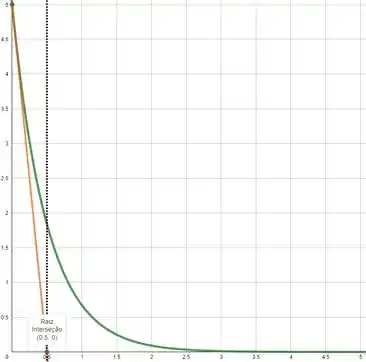
Vemos que por enquanto, o enunciado se mostrou correto, o ponto de intersecção da reta tangente ao gráfico com o eixo é .
Passo 3
Agora que entendemos, vamos testar em outro ponto qualquer do gráfico, vamos tentar em .
, e
Vamos plotar o gráfico nesse caso.
Se e , nesse caso, a verificação é satisfeita, então provamos que a intersecção entre a reta tangente de com o eixo das abscissas possui um valor de .
Foi de boa? Bora pra mais uma!
Resposta
Resposta no decorrer do passo-a-passo.