Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 92a

Considere o oscilador da Figura 10.13 4 uma um AOP ideal.

  1. Calcule o valor mínimo de R 0 que fará ocorrer a oscilação.
  2. Determinação a frequência de oscilação.

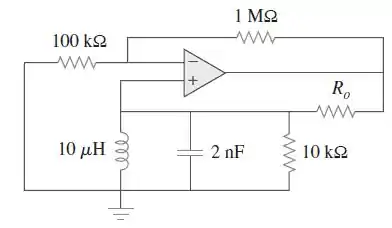
Passo 1

O circuito está representado abaixo, com nome nos nós e na impedância Z p :

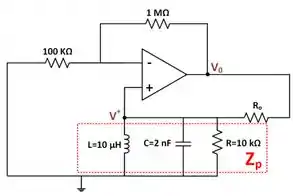
Assim, o valor de Z p é:

Z p = j ω L | | 1 j ω C | | R

Z p = ω R L ω L + j ω 2 L C - 1 R

Aplicando o divisor de tensão no terminal não inversor V + :

V + = Z p Z p + R 0 V 0

V + = ω R L ω L + j ω 2 L C - 1 R ω R L ω L + j ω 2 L C - 1 R + R 0 V 0

V + = ω R L ω L + j ω 2 L C - 1 R ω R L + ω R 0 L + j ω 2 L C - 1 R 0 R ω L + j ω 2 L C - 1 R V 0

V + = ω R L ω L + j ω 2 L C - 1 R × ω L + j ω 2 L C - 1 R ω R L + ω R 0 L + j ω 2 L C - 1 R 0 R V 0

V + = ω R L ω R L + ω R 0 L + j ω 2 L C - 1 R 0 R V 0

V + deve estar em fase com V 0 para satisfazer o segundo critério e Barkhausen. Isso implica que a razão a equação acima deve ser puramente real. Fazendo a parte imaginária ser igual a zero, podemos obter a frequência de oscilação:

ω 2 L C - 1 = 0

ω = ω 0 = 1 L C

Passo 2

O ganho é igual a:

A V = 1 + 10 6 10 5 = 11

Na frequência de oscilação,

V + V 0 = R R 0 + R

R R + R 0 = 1 11

R 0 = 100   k Ω

Resposta

O resistor é igual a:

R 0 = 100   k Ω

Ver Outros Exercícios desse livro