Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 6

A corrente através de um capacitor de 0,01F é como indicado na figura. Calcule a tensão v e a potência em t = 10ms e em t = 40ms, se v(0) = 0.

Passo 1

Iae, meus queridos! Td certinho?

A questão nos deu o gráfico de corrente pelo tempo e vamos utilizar duas equações para resolver esse exercício:

v t = 1 C ∫ i d t e P = C v 2 2

Sabemos que integral é a área abaixo da curva, agora ficou fácil.

v t = 1 0,01 · a r e a   a b a i x o   d a   c u r v a

Para t = 10ms:

Vamos calcular essa área. O gráfico não nos deu o valor de i quando t = 10ms, mas como se trata de uma reta podemos usar uma regra de 3 simples e descobrir o valor de i nesse instante.

30 - 12

10 - y 1

y 1 = 4

Assim como podemos ver em outro gráfico.

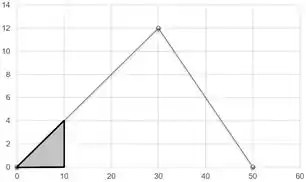
Então a área é 10 · 4 / 2 = 20 , portanto:

v t = 1 0,01 · 20

v t = 2000 V .

Já a potência:

P = 0,01 · 2000 2 2

P = 20 k J .

Passo 2

Já para t = 40ms:

A área abaixo da curva ∫ i d t é área 1 + área 2.

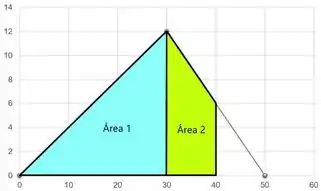
Temos ∫ i d t = 450 , portanto.

v t = 1 0,01 · 450

v t = 45 k V .

A potência nesse instante:

P = 0,01 · 45 k 2 2

P = 10125 k J .

Resposta

Para t = 10ms: v t = 2000 V .

P = 20 k J .

Para t = 40ms: v t = 45 k V .

P = 10125 k J .

Exercícios de Livros Relacionados

O pulso triangular de corrente mostrado naFigura P6.14 é aplicado a um capacitor de200 mF.a) Escreva as expressões que descrevemv(t) nos cinco intervalos t , 0, 0 # t # 2 s,2 s # t # 6 s, 6 s # t # 8
O pulso triangular de corrente mostrado na Figura P6.14 é aplicado a um capacitor de200 mF.a) Escreva as expressões que descrevem v(t) nos cinco intervalos t0 ,0t2 s , 2 st6 s , 6 st8 set8 s .b) Deduz
Sabe-se que a tensão nos terminais do capacitor da Figura 6.10 é:Faça um gráfico do pulso de corrente conduzido pelo capacitor durante o intervalo de 4 s.Suponha C = 120 mF.a) Determine a corrente no