Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 60

a) Determine a corrente i o no circuito da Figura P4.60 fazendo uma série de transformações de fonte adequadas.

b) Usando o resultado obtido em (a), faça os cálculos no sentido inverso para determinar a potência desenvolvida pela fonte de 50 V.

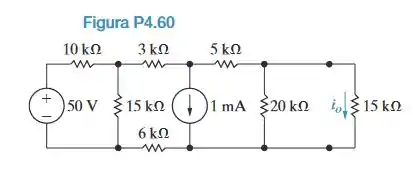
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A – Primeiramente, fazendo a transformação de fonte para a fonte de tensão de 50   V com o resistor, nós obtemos que o resistor de 15   k está em paralelo com esse mesmo resistor de 10   k , logo

15 ∙ 10 15 + 10 = 150 25 = 6   k Ω

Agora, vamos retornar a transformação, só que com o resistor de 6   k Ω , logo

5   m A × 6   k Ω = 30   V

Com isso, o circuito fica da seguinte forma, lembrando que uma associação em série entre três resistores nesse caso ( 6   k Ω ,   6   k Ω   e   3   k Ω ), logo,

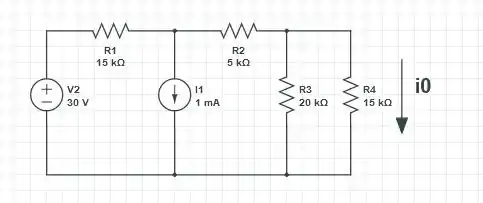
A fonte de 30   V   que está em série com o resistor de 15   k Ω está sendo convertida para 2   m A em paralelo com o mesmo resistor de 15   k Ω . Esta fonte de corrente subtrai com a fonte de corrente de 1   m A , logo

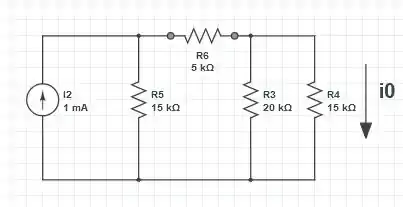
Passo 2

Advinha o que nós vamos fazer novamente? Isso mesmo, transformação de fontes, a fonte de corrente de 1   m A passa a ser uma fonte de tensão de 15   V , com isso, temos que o resistor de 15   k Ω está em série com o resistor de 5   k Ω , logo

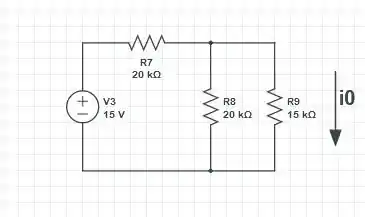
Novamente, a fonte de tensão de 15   V passa a ser uma fonte de corrente de 0,75   m A , então temos que o resistor de 20   k Ω está em paralelo com o resistor de 20   k Ω , o que nos fornece 10   k Ω

20 × 20 20 + 20 = 400 40 = 10   k Ω

Logo, o circuito fica da seguinte forma

Por divisor de corrente, podemos encontrar i 0 , logo, temos que

i 0 = 0,75 × 15 15 + 20 = 0,3   m A

Passo 3

B – Da letra a, temos que

V 1 = 0,3   m A × 15   k Ω = 4,5   V

E temos que as correntes podem ser representadas da seguinte forma,

I 1 = V 1 20   k Ω = 4,5 20   k Ω = 0,225   m A

E

I 2 = I 1 + i 0 = 0,3 + 0,225 = 0,525   m A

Pela Lei de Ohm, nós temos que

V 2 = V 1 + I 2 × 5   k Ω = 4,5 + 0,525 × 5 = 7,125   V

No nó 2, pela Lei de Kirchoff das correntes,

I 3 = 1 + I 2 = 1 + 0,525   m A = 1,525   m A

Temos que

V 4 = 0 - I 3 × 6 = 0 - 1,525 × 6 = - 9,15   V

E

V 3 = V 2 + I 3 × 3   k Ω = 7,125 + 1,525 × 3 = 11,7   V

Com isso, temos que I 4 é igual a

I 4 = V 3 - V 4 15   k Ω = 11,7 - ( - 9,15 ) 15   k Ω = 1,39   m A

Passo 4

No nó 3, novamente pela LKC, nós temos que

I s = I 4 + I 3 = 1,39 + 1,525 = 2,915   m A

Portanto, a potência fornecida pela fonte de 50   V é

50 × 2,915   m A = 145,75   m W

Resposta

a )   0,3   m A

b )   145,75   m W

Exercícios de Livros Relacionados

Determine a corrente id do detector da ponte desequilibrada da Figura P3.53, se a queda de tensão no detector for desprezível.
No circuito da ponte de Wheatstone mostrado na Figura 3.26, a razão R2/R1 pode ser ajustada para os seguintes valores: 0,001, 0,01, 0,1, 1, 10, 100 e 1.000. O resistor R3 pode variar de 1 a 11.110 V e