Em um diodo a vácuo, os elétrons são emitidos por aquecimento de um catodo, em potencial zero, e acelerados por uma distância até o anodo, que é mantido em um potencial positivo . A nuvem de elétrons em movimento (chamada carga espacial) rapidamente se acumula ao ponto em que reduz o campo na superfície do catodo a zero. A partir daí, uma corrente estacionária flui entre as placas.
Suponha que as placas sejam grandes se comparadas à separação ( na Figura 2.55), de forma que os efeitos de bordas podem ser negligenciados. Então , e (a velocidade dos elétrons) são todas funções somente de x.
a) Escreva a equação de Poisson para a região entre as placas.
b) Presumindo que os elétrons partem do repouso, qual é a sua velocidade no ponto x, onde o potencial é ?
c) No estado estacionário. é independente de . Qual é, nesse caso, a relação entre e ?
d) Use estes resultados para obter uma equação diferencial para , eliminando e .
e) Resolva esta equação para como função de , e . Faça um gráfico de e compare-o ao potencial sem carga espacial. Encontre também e como funções de .
f) Mostre que
E encontre a constante . (A Equação 2.56 é chamada de lei de Child-Langmuir. Ela também vale para outras geometrias, sempre que a carga espacial limita a corrente. Observe que o diodo limitado pela carga espacial é não linear – ele não obedece à lei de Ohm.)
Passo 1
Faaala, pessoal! Bora matar essa questão (imensa por sinal hahaha).
a) Para o item a), foi pedido que escrevêssemos a equação de Poisson para a região entre as placas. Para isso, basta nos lembrarmos da equação de Poisson que é dada por:
Logo, a equação de Poisson para a região entre as placas, será dada pela igualdade entre o Laplaciano da função do potencial e a razão entre a densidade de carga e a constante permissividade :
Passo 2
b) Na letra b), o enunciado nos pede para mostrar a velocidade dos elétrons no ponto , onde o potencial é , partindo do repouso. Como teremos a transformação da energia potencial elétrica em energia cinética (movimento dos elétrons), poderemos igualar a energia potencial elétrica com a energia cinética:
E isolando a varável da velocidade , teremos:
Passo 3
c) No item c) é pedido a gente encontre a relação entre a densidade de carga e a velocidade dos elétrons no estado estacionário, sabendo que nessas condições é independente de . A carga será dada pelo produto da densidade de carga pela área das placas:
Como sabemos, a corrente é igual a variação da carga pelo tempo, logo:
Logo, derivando a expressão da carga, teremos:
E aplicando esse resultado na expressão da corrente:
Como sabemos que a velocidade é igual a variação da distância pelo tempo:
Passo 4
d) O item d), pede para que a gente obtenha uma equação diferencial para , a partir dos resultados anteriores, eliminando e . Vamos utilizar o Laplaciano do potencial encontrado no item a) e substituir a densidade de carga pela relação que encontramos no item c)
Agora, podemos substituir o pela expressão encontrada no item b):
Para simplificar a expressão, vamos chamar e com isso, teremos:
Passo 5
e) O item e) nos pede para resolver essa equação diferencial para como função de , e e ao final fazer um gráfico de comparando o ao potencial sem carga espacial. Inicialmente, podemos fazer:
Logo:
Integrando os dois lados, teremos:
Resolvendo as integrais, teremos:
Em que é uma constante
Para a constante será 0, logo:
Agora, integrando essa expressão, teremos:
Resolvendo as integrais:
E como vimos anteriormente que a constante também será 0, logo:
E rearrumando:
Substituindo o pela expressão do item d):
Em termos de :
Sem a carga espacial expressão de , será:
E como podemos ver, nesse caso o potencial cresce linearmente! O gráfico ficará da seguinte forma:
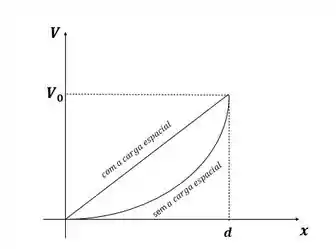
Temos do item a) que a expressão para a densidade de carga tem a seguinte forma:
Substituindo pela expressão encontrada anteriormente:
Portanto:
Para a expressão de em função de vamos utilizar a a expressão encontrada no item b):
Substituindo :
Passo 6
f) Por fim para o item f) o enunciado nos pede para encontrar a constante da equação:
Para isso, vamos manipular a expressão de encontrada no item e) para obtermos uma expressão para :
Aplicando a raiz na equação da corrente , teremos:
Igualando à equação (1):
Portanto:
E aqui finalizamos a questão, galera! Até a próxima 😊
Resposta
a)
b)
c)
d)
e)
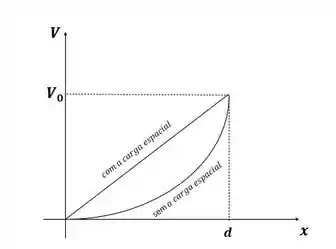
f)