Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 21

C a l c u l e o v a l o r e f i c a z d a t e n s ã o v e m r e g i m e p e r m a n e n t e .

Passo 1

E aí gurizada tudo belezinha? O enunciado pede que a gente determine o valor da tensão, então vem comigo para trazer novamente o circuito expresso no enunciado :)

Superposição

omega = 2

i_1 = 2 /_ 0

v^' = 2 i_1 * 4 /_ 0

v^' = 4 c o s 2 + v

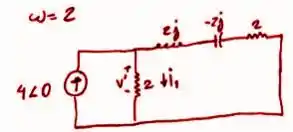
Passo 2

Em circuitos lineares cujas entradas são funções periódicas no tempo, as tensões e correntes em regime permanente produzidas são periódicas

omega = 4

v^(' ') = (10 * 2)/(4 + 3 ȷ) - 4 /_ - 36 , 87^@

V^(' ') = 4 c o s (4 t - 36 , 87^@) V

V_R M S = V_(R m S )^' + V_(A A s )^(' ')

V_R M S = sqrt((4^2)/(2) + (4^2)/(2)) = sqrt(16) = 4 V_r M s

Resposta

4 V_r M s

Exercícios de Livros Relacionados

Mostre que, para 0 circuito do Ex. 15.4.1, a energia dissipada por ciclo e ∫ 0 2 π w 0 R I M 2 cos 2 ⁡ w 0 t d t = π R I M 2 w 0 e, desta forma, pela definição (15.27) e 0 resultado do Ex. 15.4.1. que
O amp op no circuito da Figura P10.7 é ideal. Calcule a potência média fornecida ao resistor de 1 kV, quando v g=c o s1.000 tV .