Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 8

Escolha C = 0.1 μ F e calcule R e L no Prob. 15.6, de forma que ω 0 = 10 4 rad/s e B = 10 4 rad/s.

Passo 1

Primeiramente, o circuito que a questão está mencionando é este:

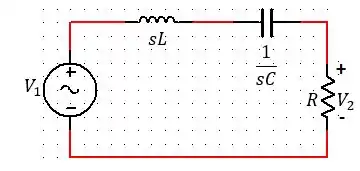
Pela Lei de Ohm a corrente nesse circuito será:

i = V 1 s L + 1 s C + R

Assim, V 2 é dado por:

V 2 = R i ∴

V 2 = R   V 1 s L + 1 s C + R ∴

V 2 V 1 = s R C s 2 L C + s R C + 1 ∴

V 2 V 1 = s R L s 2 + s R L + 1 L C = H ( s )

Como C = 0.1 μ F , temos que:

V 2 V 1 = s R L s 2 + s R L + 1 L 10 - 7 = H ( s )

Passo 2

Nesse sentido, percebemos que H ( s ) tem o formato de:

K s s 2 + B s + ω 0 2

Logo, temos que:

K = R L

B = R L

ω 0 = 1 L C

Passo 3

Sabemos que ω 0 = 10 4 rad/s e C = 0.1 μ F . Assim, temos:

10 4 = 1 L 10 - 7 ∴ L = 0.1   H

Passo 4

Também sabemos que B = 10 4 rad/s e que L = 0.1   H . Assim, temos:

10 4 = R 0.1 ∴ R = 1   k Ω

Facinho demais né?? Vamos para a próxima!! ;)

Resposta

L = 0.1   H

R = 1   k Ω

Exercícios de Livros Relacionados

Mostre que a frequência de ressonância. no caso da função do Ex. 15.2.1, coincide com a frequência para a qual a função e real.
No Ex. 15.3.2(a), calcule a amplitude para a tensão na associação se a fonte de corrente é i g = cos ⁡ ω t mA e ω é (a) 10 4 , (b) 5 · 10 4 e (c) 25 · 1 0 4r a d / s .
Faça a resposta em amplitude | H ( j ω ) | ser tal que H j ω M a x = H j 0 = K , de forma que no corte H j ω c = K / 2 . Calcule a perda, dada por (15.38), em ω = 0 e em ω = ω c . Note que ω c corresp
Dada a função do filtro passa-faixa calcule as perdas em decibéis em ω = 0,0001 ;0,5 ;0,905 ;1,0 ;1,105 ;10e100r a d / s .
Uma tensão senoidal de 400 Hz, com amplitude máxima de 100 V em t = 0, é aplicada aos terminais de um indutor. A amplitude máxima da corrente de regime permanente no indutor é 20 A. a) Qual é a frequê