Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 61

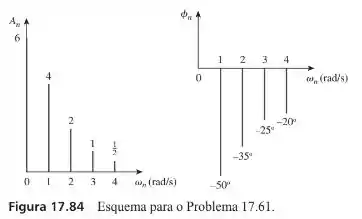
Os espectros das séries de Fourier de uma função são mostrados na Figura 17.84.

a Obtenha a série de Fourier trigonométrica.

b Calcule o valor RMS da função.

Passo 1

Para encontrarmos a série de Fourier trigonométrica para a função mostrada na figura vamos utilizar a seguinte fórmula

f t = a 0 + ∑ A n ⋅ cos ⁡ n ⋅ ω 0 ⋅ t - ϕ n

Onde, para nosso caso vamos ter o n variando de 1   a   4 e nosso a 0 = 6 . Dessa forma, podemos escrever f t como sendo

f t = 6 + 4 ⋅ cos ⁡ t + 50 + 2 ⋅ cos ⁡ 2 t + 35 ° + cos ⁡ 3 t + 25 ° + 1 2 ⋅ cos ⁡ 4 t + 20 °

É possível escrever de uma forma mais compacta expandindo nossa expressão com as equações de soma de arcos, mas escrita dessa forma fica mais agradável e simples de entender como é construído o raciocínio para obtenção das mesmas através dos gráficos.

Passo 2

Por fim, para encontrarmos o valor R M S da nossa função vamos utilizar a seguinte fórmula

f r m s = a 0 2 + 1 2 ⋅ ∑ n = 1 ∞ A n 2

Dessa forma, aplicando para os nossos dados teremos

f r m s 2 = 6 2 + 1 2 ⋅ 4 2 + 2 2 + 1 2 + 1 2 2 = 46.625

f r m s = 46.625 ≈ 6.828

E está concluído nosso exercício.

Resposta

a   f t = 6 + 4 ⋅ cos ⁡ t + 50 + 2 ⋅ cos ⁡ 2 t + 35 ° + cos ⁡ 3 t + 25 ° + 1 2 ⋅ cos ⁡ 4 t + 20 °

b f r m s =   6.828

Ver Outros Exercícios desse livro