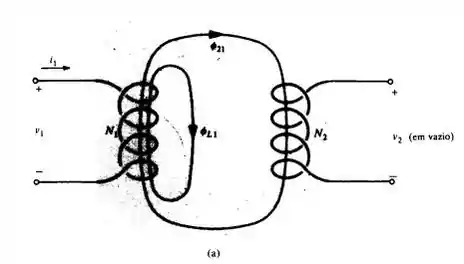
Na Fig. 16.2(a), espiras e , quando . Determine se .
Passo 1
E aí gurizada tudo belezinha? O enunciado pede que a gente determine se .
Vamos esboçar o circuito
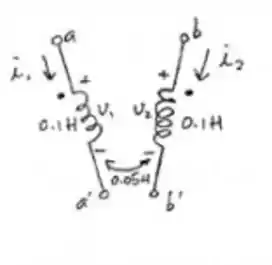
Agora podemos relacionar os ângulos
Na Fig. 16.2(a), espiras e , quando . Determine se .

E aí gurizada tudo belezinha? O enunciado pede que a gente determine se .
Vamos esboçar o circuito

Agora podemos relacionar os ângulos