Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.5 - Ex. 4

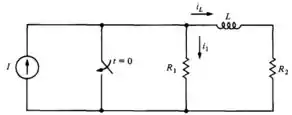
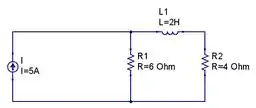
Na Fig. 7.10, seja I = 5 A, R1 = 6𝝮, R2 = 4 𝝮, L = 2H, e i1(0-) = 2 A. Se a chave é aberta em t = O-, encontre iL(0-), iL(0+), i1(0+) e diL(0+)/dt.

Passo 1

Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrar as correntes em momentos em que a chave está aberta e fechada. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??

Passo 2

Ok, vamos logo para o item a).

Analisando o circuito no momento em que t =   0 - , ou seja, quando a chave está aberta. Assim, temos que

Agora o nosso problema vai ser resolvido usando LKC, no nó de divisão de i L   e   i 1 , assim

I = i L + i 1

5 = i L + 2

i L ( 0 - ) = 3   A

Agora, analisando o circuito no momento em que t =   0 + , ou seja, quando a chave está fechada. Assim, temos que

Nesse momento temos que o indutor não permite a variação brusca de corrente, assim:

i L 0 + = i L ( 0 - ) = 3   A

Bora para o item b).

Analisando o circuito no momento em que t =   0 + , ou seja, quando a chave está fechada. Assim, temos novamente que

Podemos ver que a corrente que passava por R1, agora passa pelo curto-circuito, resultando em

i 1 ( 0 + ) = 0   A

Passo 3

Finalizando agora com o item d).

Como já sabemos que em t =   0 + , i 1 ( 0 + ) = 0   A e i L 0 + = 3   A , assim pela Lei de Ohm podemos encontrar a tensão em R2, portanto:

v 2 = 3   ∙ 4 = 12   V

Agora pela LKT, descobrimos a tensão no indutor

v L + v 2 + v 1 = 0

v L =   - 12   V

Para finalizar, temos que lembrar a relação entre a tensão e a corrente em um indutor. Lembra?? Responde Aí!!!

v = L ∙ d i d t

Portanto substituindo os valores já encontrados, temos que

d i ( 0 + ) d t = v L =   - 12 2   =   - 6   A / s

Tranquilo essa hein!!

Resposta

i L ( 0 - ) = 3   A

i L ( 0 + ) = 3   A

i 1 ( 0 + ) = 0   A

d i ( 0 + ) d t = - 6   A / s

Exercícios de Livros Relacionados

Determine a L e q nos terminais a - b do circuito da figura 6.73.
A tensão em um indutor de 200 m H é dada por v t = 3 t 2 + 2 t + 4V p a r at0 Determine a corrente i t que passa pelo indutor. Suponha que i 0 = 1 A .
Usando a figura 6.74, elabore um problema para ajudar os outros estudantes a entenderem melhor como os indutores se comportam quando conectados em série e quando conectados em paralelo.
No circuito da figura 6.82, i_o (0) = 2 A . Determine i_0 (t) e v_0 (t) para t0 .
A forma de onda da corrente na figura 6.80 percorre um indutor de 3 H . Esboce a tensão através do indutor ao longo do intervalo 0t6 s .