Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 6.Problemas - Ex. 10
A figura do Ex. e as figuras (a) e (b) mostradas aqui sāo exemplos de um gráfico de rede escada. Existe um teorema que estabelece que o número de árvores num gráfico de escada de ramos é o número de Fibonacci , definido por , etc. Isto é, exceto e , cada número de Fibonacci é obtido da soma dos dois anteriores. Demonstre que o teorema se verifica para os gráficos de escada mostrados e também para o gráfico da figura do Ex. 6.2.2.
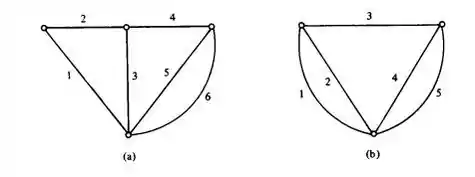
Passo 1
E ai gurizada tudo belezinha? O exercício pede que a gente demonstre que o teorema se verifica para os gráficos de escada mostrados e também para o gráfico da figura do Ex. 6.2.2.
Deixe satisfazer
somando as m equações e agrupando por ordens de derivadas
Ou
A equação forçada é
Resposta
Exercícios de Livros Relacionados
18- Use o método das tensões de nó para calcular a potência gerada pela fonte de tensão dependente no circuito da Figura P4.18.Figura P4.18
19- a) Use o método das tensões de nó para determinar a potência total gerada no circuito da Figura P4.19. b) Verifique sua resposta determinando a potência total absorvida no circuito. Figura P4.19
21-a) Determine as tensões de nó v1, v2 e v3 no circuito da Figura P4.21. b) Determine a potência total dissipada no circuito. Figura P4.21
27-a) Use o método das tensões de nó para determinar as correntes de ramo i 1, i 2 e i 3 no circuito da Figura P4.27. b) Verifique sua solução para i 1, i 2 e i 3, mostrando que a potência dissipada n
24-Use o método das tensões de nó para determinar i o no circuito da Figura P4.24.Figura P4.24