Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Eletrodinâmica - David J. Griffiths- Ed: 3º - Capítulo 3.Problemas - Ex. 39

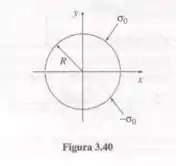
Uma longa casca cilíndrica de raio R tem uma densidade superficial de carga uniforme σ 0 na metade superior e uma densidade de carga oposta - σ 0   na metade inferior (Figura 3.40). Encontre o potencial elétrico dentro e fora do cilindro.

Passo 1

Olá pessoal, bora para mais uma!?

Para começar a pensar nesta questão podemos usar informações que já obtivemos anteriormente no livro, com isso podemos separar as variáveis do potencial calculado no problema 3.23 em coordenadas cilíndricas, com isso temos que:

V s , ϕ = a 0 + b 0 ln ⁡ s + ∑ k = 1 ∞ [ s k a k c o s k ϕ + b k s i n k ϕ + s - k ( c k c o s k ϕ + d k s i n k ϕ ) ]  

Porém temos a separação do potencial dentro e do potencial fora, assim:

Para s

V s , ϕ = ∑ k = 1 ∞ [ s k a k c o s k ϕ + b k s i n k ϕ ]  

Para s>R, temos:

V s , ϕ = ∑ k = 1 ∞ [ s - k ( c k c o s k ϕ + d k s i n k ϕ ) ]  

E continuando para s=R, temos que:

∑ R k a k c o s k ϕ + b k s i n k ϕ = ∑ [ R - k ( c k c o s k ϕ + d k s i n k ϕ ) ]

Aqui temos algumas conclusões: c k = R 2 k a k ,   d k = R 2 k b k , e como pela eq. 2.36, podemos dizer que:

∂ V ∂ s R + -   ∂ V ∂ s R - = - 1 ϵ 0 σ

Passo 2

Assim podemos reescrever a expressão para o potencial, como:

∑ - k R k + 1 a k c o s k ϕ + b k s i n k ϕ - ∑ k R k - 1 c k c o s k ϕ + d k s i n k ϕ = - 1 ϵ 0 σ

Reescrevendo a expressão acima, temos:

∑ 2 k R k - 1 a k c o s k ϕ + b k s i n k ϕ = σ 0 / ϵ 0 ,       0 < ϕ < π - σ 0 / ϵ 0 ,       π < ϕ < 2 π

Pelo truque de Fourier. Começando multiplicando por cos ⁡ l ϕ d ϕ e integremos de 0 a 2 π , temos:

∫ 0 2 π s i n k ϕ c o s l ϕ d ϕ = 0 ,         ∫ 0 2 π c o s k ϕ cos ⁡ l ϕ d ϕ = 0 ,         k ≠ l π ,         k = l

Então:

2 l R l - 1 π a l = σ 0 ϵ 0 ∫ 0 π c o s l ϕ d ϕ - ∫ π 2 π c o s l ϕ d ϕ = σ 0 ϵ 0 s i n l ϕ l 0 π - s i n l ϕ l π 2 π = 0 ,  

A s s i m   a l = 0

Agora multiplicamos por sin ⁡ l ϕ d ϕ , e integrando de 0 a 2 π , temos:

∫ 0 2 π s i n k ϕ s i n   l ϕ d ϕ = 0 ,         k ≠ l π ,         k = l

Então:

2 l R l - 1 π B l = σ 0 ϵ 0 ∫ 0 π s i n l ϕ d ϕ - ∫ π 2 π s i n l ϕ d ϕ = σ 0 ϵ 0 - c o s l ϕ l 0 π + c o s l ϕ l π 2 π

= σ 0 l ϵ 0 2 - 2 cos ⁡ l π = 0   s e   l   f o r   p a r 4 σ 0 / l ϵ 0   s e   l   f o r   í m p a r  

Portanto temos que:

b l = 0   s e   b l   f o r   p a r 2 σ 0 / π ϵ 0 l 2 R l - 1   s e   l   f o r   í m p a r

E assim podemos concluir que o potencial é:

V s , ϕ = 2 σ 0 R π ϵ 0 ∑ k = 1,3 , 5,7 … 1 k 2 s i n k ϕ s R k , s e   s < R R s k , s e   s > R

Assim finalizamos mais uma! Até a próxima!

Resposta

V s , ϕ = 2 σ 0 R π ϵ 0 ∑ k = 1,3 , 5,7 … 1 k 2 s i n k ϕ s R k , s e   s < R R s k , s e   s > R

Resposta

Ei, a resposta está no passo a passo :)