Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 28

Mostre, calculando H = V 2 / V 1 , que o circuito dado é um filtro passa-faixa e calcule a freqüência central e a faixa de passagem. Altere em escala o circuito de forma que a freqüência central seja 20.000 r a d / s , usando capacitores de 0,01 μ F .

Passo 1

O enunciado pede que a gente encontre galera calculando H = V 2 / V 1 , que o circuito dado é um filtro passa-faixa e calcule a freqüência central e a faixa de passagem.

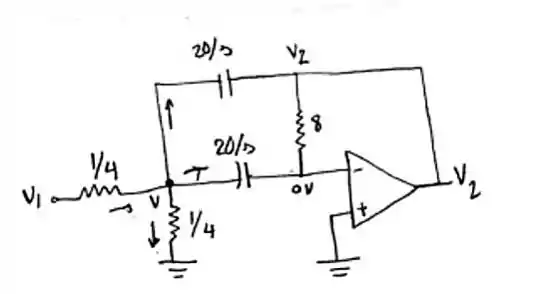
Começamos a esboçar o circuito do enunciado para facilitar os cálculos 😊

V - V 2 ⇒ - 5 V 2 20 - V 2

⇒ V 2 - 5 + 25 20

V 20 / s = - V 2 8 ⇒ D V 5 = - V 2 2 ⇒ 2 s V = - 5 V 2 ⇒ V = - 5 V 2 2 s

V 1 + 5 V 2 2 2 1 4 = - 5 V 2 2 s 1 4 + - 5 V 2 20 - V 2 20 s - 5 V 2 2 π s ⋅ 25 20 ⇒

⇒ 2 , V 1 - 5 V 2 2 s 3 ⋅ y = - 5 V 2 ⋅ x ⧸ 2 s + 1 - 5 V 2 - 3 V 2 2 s ⋅ s 20 - V 2 8 ⇒

⇒ 4 Δ s V z - 10 V 2 s = - 10 V 2 s - V 2 8 - 5 V 2 - 2 s V 2 40 ⇒ 16 c o s ⁡ V 1 40 / s = = - 800 V 2 - 50 V 2 - 50 V 2 - 23 2 V 2 40 / s ⇒

⇒ 160 s V 1 = V 2 - 2 s 2 - 10 s - 800 ⇒ V 2 V 1 = - 80 s 2 s 2 + 10 s + 900

ω 0 i = 20 r a d / s

Passo 2

Alterar a escala

ω 0 f = 20000 r a d s                     k f = 10 3 C = 0,01 u F

ω a j = 20 r a d / s

c = c ' k i K f ⇒ K i = 0,05 0,01 ⋅ 10 - 6 ⋅ 10 3 = 5000

R ( 1 / 4 ) = K i ⋅ 1 / 4 = 1,25 K Ω

R ( 8 ) = K i ⋅ 8 = 40 K Ω

Resposta

40 K Ω