Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 37

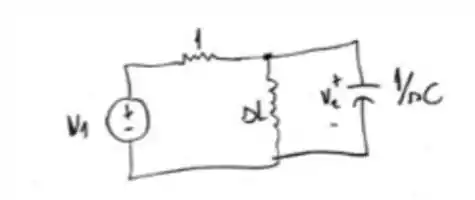
Mostre, calculando a função de rede H ( s ) = V 2 ( s ) / V 1 ( s ) , que o circuito é um filtro passa-faixa com ω 0 2 = 1 / ( L C ) , B = 1 / C e ganho = 1 . Escolha L e C de forma que B = 0,2   e   ω 1 = 1 r a d / s .

Passo 1

O exercício pede que a gente calcule a função de rede H ( s ) = V 2 ( s ) / V 1 ( s ) , que o circuito é um filtro passa-faixa com ω 0 2 = 1 / ( L C ) , B = 1 / C e ganho = 1 . Escolha L e C de forma que B = 0,2   e   ω 1 = 1 r a d / s .

Vamos começar esboçando o circuito 😊

V 1 - V 2 1 = V 2 s L + V 2 s C ⇒ V 1 = V 2 1 + 1 s L + s C ⇒

⇒ V 1 V 2 = s L + 1 + s 2 L C s L ⇒ V 2 V 1 = s L s 2 L + s L + 1 = s / C s 2 + s C + V L C

B = 0,2 ⇒ 0,2 = 1 / C ⇒ C = 5 F

ω 0 = 1 ⇒ 1 2 = 1 / L C ⇒ L C = 1 ⇒ L = 1 / C = 0,2

H ω j = j ω L - ω 2 L C + j ω L + 1 = 1 1 + j ω C - 1 ω l = 1 1 + j 5 ω - 5 ω

Passo 2

l i m ω → 0   1 1 + j 5 ω 0 - s b = 1   l i m ω ∞   = 1 1 + j 5 ω - 5 ω =

ω 0 2 = 1 L C B = 1 C G = K a = 1 / C 1 / C = 1

Resposta

G = 1

Exercícios de Livros Relacionados

Use os resultados do Prob. 15.24 para projetar um filtro corta-faixa com ω 0 = 1 r a d / s , Q = 2 e um ganho de 1 / 2 .
Altere em escala a impedância e a frequência no circuito do Prob. 15.1c o mR = 1 Ω , L = 0,5 H e C = 0,02F para obter um filtro passa-faixa com freqüência central f 0 = 10 5H z , com índice de mérito
Mostre que a função de rede do circuito dado é H ( s ) = V 2 V 1 = K s 2 + 1 s 2 + ( 1 / Q ) s + 1 Desta forma o circuito é um filtro corta-faixa com frequência central (rejeição) ω 0 = 1 r a d / s .
Mostre, calculando H = V 2 / V 1 , que o circuito dado é um filtro passa-faixa e calcule a freqüência central e a faixa de passagem. Altere em escala o circuito de forma que a freqüência central seja
Mostre que a função de transferência V 2 / V 1 é dada por H ( s ) = V 2 ( s ) V 1 ( s ) = 1 R 1 s s 2 + 1 R 2 s + 1 R 3 Calcule R 1 , R 2 e R 3 de forma a que a funçăo de transferėncia seja idéntica á