Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 96

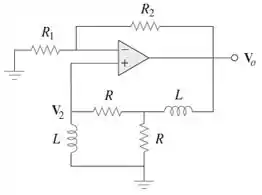
Observe o oscilador da Figura 10.137 .

  1. Demonstre que

    2. V 2 V 0 = 1 3 + j ω L R - R ω L

  2. Determine a frequência de oscilação f 0
  3. Obtenha a relação entre R 1 e R 2 de modo que ocorra a oscilação.

Passo 1

Bom, galera, para o circuito abaixo, aplicando a lei dos nós no nó V 2 , temos:

V 2 j ω L + V 2 - V x R = 0   →     V 2 1 j ω L + 1 R = V x R

V 2 R + j ω L j ω L R = V x R

V 2 R + j ω L = j ω L V x

V x = R + j ω L j ω L V 2 … ( 1 )

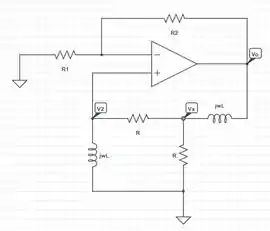
Aplicando a lei dos nós no nós V x , temos:

V x - V 2 R + V x R + V x - V 0 j ω L = 0   →     V x 1 j ω L + 2 R - V 2 R = V 0 j ω L

Multiplicando a equação anterior por j ω L R .

V x R + j 2 ω L - j ω L V 2 = R V 0 … ( 2 )

Substituindo a equação ( 1 ) na equação ( 2 ) ,

R + j ω L j ω L R + j 2 ω L V 2 - j ω L V 2 = R V 0

Multiplicando a equação por j ω L ,

R + j ω L R + j 2 ω L V 2 + ω 2 L 2 V 2 = j ω L R V 0

R 2 + j 3 ω L R - 2 ω 2 L 2 + ω 2 L 2 V 2 = j ω L R V 0

V 2 V 0 = j ω L R R 2 - ω 2 L 2 + j 3 ω L R

V 2 V 0 = 1 R 2 j ω L R   - ω 2 L 2 j ω L R + 3

V 2 V 0 = 1 3 + j ω L R - R ω L … ( 3 )

Passo 2

Na letra (b), para satisfazer o segundo critério de Barkhausen, V 2 deve estar em fase com V 0 , o que implica que a razão da equação ( 3 ) deve ser puramente real. Logo, a parte imaginária deve ser igual a zero.

ω 0 L R - R ω 0 L = 0   →   ω 0 L R = R ω 0 L

ω 0 2 = R 2 L 2

ω 0 = R L   →     2 π f 0 = R L

f 0 = R 2 π L

Passo 3

De acordo com a equação ( 3 ) , em ω = ω 0 :

V 2 V 0 = 1 3

Assim, para satisfazer o primeiro critério de Barkhausen, o amp-op deve compensar provendo ganho de 3 ou mais para que o ganho total seja de pelo menos uma unidade. Lembrando que para amplificadores não inversores:

V 0 V 2 = 1 + R 2 R 1 = 3

R 2 R 1 = 2

R 2 = 2 R 1

Resposta

  1. Demonstrado no passo 1
  2. f 0 = R 2 π L
  3. R 2 = 2 R 1
Ver Outros Exercícios desse livro