Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 17.Problemas - Ex. 21

Obtenha a serie exponencial para a senoide retificada de onda completa do Ex. 17.2.3, a partir de sua série trigonométrica.

Passo 1

Nessa questão ele pede para calcular a serie exponencial para a senoide retificada de onda completa do

f t = e - t ,     - 1 < t < 1

f t + 2 = f ( t )

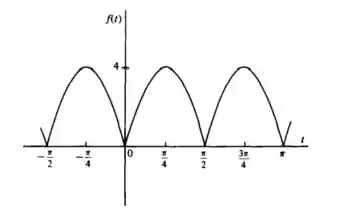
Agora vem comigo e confia em mim, blz?

Passo 2

Para determinarmos a senoide retificada temos que,

Para f ( t ) para:

a n = 4 T ∫ 0 t 2 f ( t ) cos ⁡ n w 0 t d t

b n = 0

Para f ( t ) impar:

b n = 4 T ∫ 0 t 2 f ( t ) cos ⁡ n w 0 t d t

a n = 0

Para,

cos ⁡ n w 0 t = 1 2 ( e j n w 0 t + e - j n w 0 t )

sin ⁡ n w 0 t = 1 j 2 e j n w 0 t - e - j n w 0 t

Ficando por fim analisando a imagem,

∑ n = - ∞ ∞ 8 π ( 1 - 4 n 2 ) e j 4 n t

Espero ter ajudado, até próxima.

Resposta

∑ n = - ∞ ∞ 8 π ( 1 - 4 n 2 ) e j 4 n t