Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 16.Problemas - Ex. 26

A onda quadrada de tensão da Figura P16.26(a) é aplicada ao circuito da Figura P16.26(b).a) Determine a série de Fourier da corrente i de regime permanente.b) Determine a expressão de regime permanente para i por análise elementar de circuitos.

Passo 1

[a] Expresse v g como uma constante mais uma onda quadrada simétrica. A constante é V m / 2 e a onda quadrada tem amplitude de V m / 2 , é ímpar e tem simetria de meia e quarto de onda. Portanto, a série de Fourier para v g é

v g = V m 2 + 2 V m π ∑ n = 1,3 , 5 ∞   1 n s i n ⁡ n ω 0 t

A componente dC da corrente é V m / 2 R e a k-ésima corrente de fase harmônica é

I k = 2 V m / k π R + j k ω 0 L = 2 V m k π R 2 + k ω 0 L 2 / - θ k

Em que θ k = t a n - 1 ⁡ k ω 0 L R

Assim, a série de Fourier para a corrente em regime permanente é

i = V m 2 R + 2 V m π ∑ n = 1,3 , 5 ∞   sin ⁡ n ω 0 t - θ n n R 2 + n ω 0 L 2 A

Passo 2

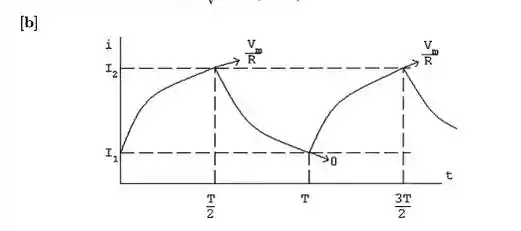
A corrente de estado estacionário alternará entre I 1 e I 2 em traços exponenciais, conforme mostrado. Assumindo que t = 0 no instante em que i aumenta em direção a   V m / R ,), temos

i = V m R + I 1 - V m R e - t / τ  for  0 ≤ t ≤ T 2

e i = I 2 e - [ t - ( T / 2 ) ] / τ for T / 2 ≤ t ≤ T , em que τ = L / R . Agora resolvemos para I 1 e I 2 por notar que

I 1 = I 2 e - T / 2 τ  and  I 2 = V m R + I 1 - V m R e - T / 2 τ

Estas duas equações estão agora resolvidas para I 1 . Fazendo x=T/2τ, obtemos

I 1 = V m / R e - x 1 + e - x

Portanto, as equações para i se tornam

i = V m R - V m R 1 + e - x e - t / τ   para   0 ≤ t ≤ T 2   e i = V m R 1 + e - x e - [ t - ( T / 2 ) ] / τ   para   T 2 ≤ t ≤ T

Uma verificação da validade dessas expressões mostra que elas produzem um valor médio de V m / 2 R

I avg  = 1 T ∫ 0 T / 2   V m R + I 1 - V m R e - t / τ d t + ∫ T / 2 T   I 2 e - [ t - ( T / 2 ) ] / τ d t

= 1 T V m T 2 R + τ 1 - e - x I 1 - V m R + I 2 = V m 2 R   uma vez que   I 1 + I 2 = V m R

Resposta

a.   i = V m 2 R + 2 V m π ∑ n = 1,3 , 5 ∞   sin ⁡ n ω 0 t - θ n n R 2 + n ω 0 L 2 A

b. V m 2 R   uma vez que   I 1 + I 2 = V m R