Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 15.Problemas - Ex. 44
a) Projete um filtro Butterworth passa-faixa
de banda larga com uma frequência de
corte inferior de 200 Hz e uma frequência
de corte superior de 2.500 Hz. O ganho na
faixa de passagem do filtro é 40 dB. O
ganho deve baixar, no mínimo, 40 dB em
40 Hz e 12,5 kHz. Use capacitores de 1 mF
no circuito passa-altas e resistores de 2,5
kV no circuito passa-baixas.
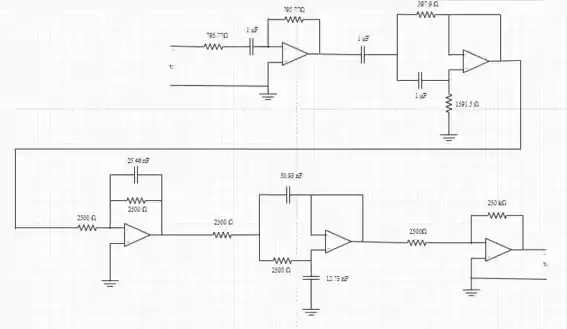
b) Desenhe o diagrama de filtro e identifi-
que todos os componentes.
Passo 1
- Projete um filtro de ganho unitário primeiro e use um amplificador inversor para fornecer o ganho de banda passante.
A frequência de corte do filtro passa-altas é igual a 200 Hz.
Determine a ordem do filtro passa-alta n,
assim sendo, o filtro de ordem n é dado por,
Então, a função de transferência do filtro passa-alta é dada por,
Sejam os valores dos resistores e do capacitor da seção de primeira ordem os seguintes,
Determine o resistor da seção de segunda ordem,
entao,
Determine o resistor da seção de segunda ordem,
determinar o fator de escala de frequência,
onde onde e são as frequências de corte escalonadas e não escalonadas, respectivamente.
Agora iremos determinar o valor do fator ,
onde C e C' são os capacitores não escalonados e escalonados do filtro passa-alta.
Determine os resistores escalados e do circuito de primeira ordem,
assim,
Determine o resistor escalado do circuito de segunda ordem,
Determine o resistor escalado do circuito de segunda ordem,
Passo 2
A frequência de corte do filtro passa-baixa é igual a 2500 Hz.
Determine a ordem do filtro passa-baixa n,
portanto, a ordem do filtro n é dada por,
então, a função de transferência do filtro passa-baixa é dada por,
Sejam os valores dos resistores e do capacitor da seção de primeira ordem os seguintes,
Determine o capacitor da seção de segunda ordem,
então,
Determine o capacitor da seção de segunda ordem,
determinar o fator de escala de frequência,
onde onde e são as frequências de corte escalonadas e não escalonadas, respectivamente.
Agora iremos determinar o valor do fator ,
Onde R e R' são os resistores não escalonados e escalonados do filtro passa-baixa.
O resistor escalado de seção de primeira ordem é dado por,
Determine o capacitor escalado C' da seção de primeira ordem,
assim,
Os resistores escalonados de sessão de segunda ordem são dados por,
Determine o capacitor escalado da seção de segunda ordem,
Determine o capacitor escalado da seção de segunda ordem,
Para o amplificador de ganho, o valor numérico do ganho de passa-banda é dado por,
Seja o resistor de entrada do amplificador de ganho como segue,
então, o resistor de feedback é dado por,
Passo 3
Resposta
- Para HPF primeira sessão
- Ver a figura
para HPF segunda sessão
para HPF segunda função
para HPF sessão
para LPF sessão
para LPF primeira sessão
para LPF segunda sessão
para LPF segunda sessão
para o ganho amplificador
para o ganho amplificador