Projete um filtro R-C passa-alta com uma frequência de corte de , usando um capacitor de . Escolha o valor comercial de mais próximo e calcule novamente a frequência de corte para o novo valor da resistência. Trace a curva do ganho normalizado na faixa de frequências de a
Passo 1
E aeeee gente! É o seguinte, vamos calcular qual deve ser o valor de no filtro passa alta para que a frequência de corte seja , sendo que o capacitor é de
A frequência de corte é calculada assim:
Substituindo os valores:
Então
Passo 2
Beleza, mas será que o valor de que encontramos é implementável na vida real?
Em uma aplicação prática, teríamos que aproximar isso usando os resistores comerciais disponíveis, e para isso fazemos:
Que são 2 resistores disponíveis no mercado hehehe
Passo 3
Para os resistores comerciais, a frequência de corte vai ser
Passo 4
Queremos traçar o gráfico de , que é calculado assim em um filtro passa altas:
Substituindo :
Onde
Pronto, essa é a equação genérica que vamos usar para calcular o em
Passo 5
Sabendo que , os valores de que vamos substituir na expressão de são
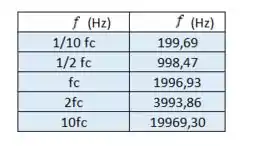
Então, substituindo esses valores de frequência na expressão , temos
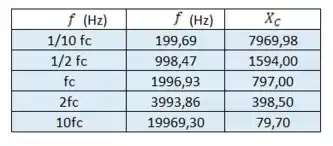
E, por fim, aplicando os dados que temos na expressão
, encontramos os valores que vamos plotar:
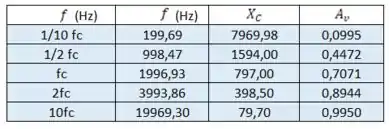
Passo 6
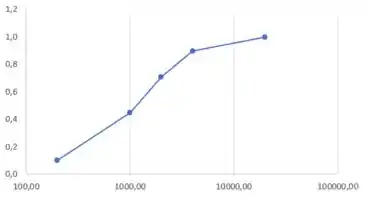
Plotando os dados da tabela anterior com escala logarítmica no eixo horizontal, temos:
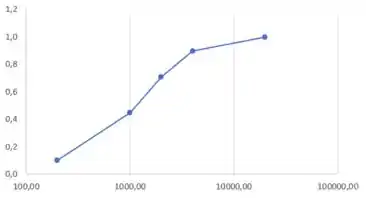
Fechou?
Resposta
Utilizando resistores comerciais, temos e