Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 4.5 - Ex. 2
Repita 0 Exerc. 4.5.1 com R1 = 1, R2 = 2, R3 = 4, vg1 = 21 V e vg2 = 0. Verifique os resultados empregando resistência equivalente e divisão de corrente.
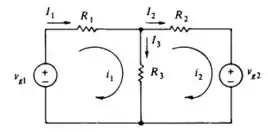
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para achar as correntes, então vamos encontrar através da análise de malha. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
Para deixar de uma maneira mais clara, vamos enumerar esse circuito
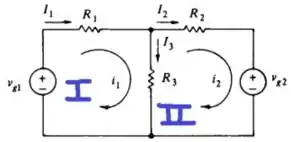
Agora já está bem mais fácil a visualização!!
Passo 2
Então vamos lá!!
Aplicando LKT na malha 1, isto resulta na equação
Agora, aplicando LKT na malha 2, isto resulta na equação
Passo 3
Vamos para o passo final!!
Agora, como já temos todos os dados disponíveis, é só resolver as equações (1) e (2).
Como temos duas incógnitas para duas equações, temos como resolver.
Isolando uma incógnita em uma equação e substituindo na outra, vamos chegar em
Agora vamos confirmar
Pelo circuito
Pela divisão de corrente
Pronto!!