Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 16.Problemas - Ex. 15

Repita o Prob, 16.13 , se omega = 4 r a d // s e t = pi // 8 s .

Passo 1

Partiu mais um exercício de circuitos, vem comigo galera!!

2 (d i_1)/(d t) + 2 (i_1 - i_g) = 0

2 s I_1 ( s ) - 2 i_1 (0 -) + 2 I_1 ( s ) - (4)/(s) = 0

I_1 ( s ) = (4)/(s) (1)/(2 ( s + 1 )) = (2)/(s ( s + 1 ))

v ( t ) = - m (d i_1)/(d t)

(V (s) = - s I_1 (s) + i ( O - )) = (- 2)/(s + 1)

:. v ( t ) = - 2 e^(- t) V

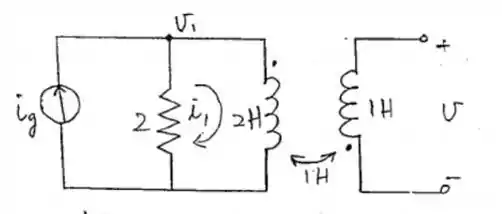
Viu como foi tranquilo?! Agora podemos ir pro próxima 😊

Resposta

v ( t ) = - 2 e^(- t) V

Exercícios de Livros Relacionados

Calcule as correntes i_1 c i_2 e m regime permanente.
Se a indutância medida entre os terminais a e d e ́ 0.1 H , quando os terminais b e c são conectados, e a indutåncia medida entre os terminais a e cé 0.9 H , quando os terminais b e d são conectados.
Calcule v , para t0 , no secundário em vazio, s c i_g = 8 u ( t )
(a) Calcule v 1 e v 2 . se L 1 = 2 H , L 2 = 5 H , M = 3 H , i 1 = 5 s e n ⁡ 2 t A e i 2 = - 3 c o s ⁡ 4 tA . (b) Calcule v 2 , se o secundário está em vazio.
Calcule no transformador da Fig. 16.3(a), quando i 1 = 2A e i 2 = 4A , se L 1 = 2 H , L 2 = 10 H e M = 4 H . (b) Repita a parte (a), se um dos pontos de polaridade for passado para o outro terminal.