Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 32

Repita o Prob. 8.25, se a fonte de 36V e substituída por uma de 36 e - 3 t V com a mesma polaridade.

Passo 1

Fala, pessoal. Tudo tranquilo?

Vocês estão mandando muito nas questões. Mas, vamos continuar praticando. Olha só esse circuito RC, a questão nos pede a corrente que está circulando na malha 1 e a tensão do capacitor de 1 8 F . Vamos fazer juntinhos e arrasar! 💪

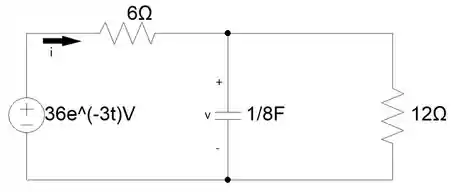
Para essa questão, temos que fazer análise de malhas, para isso vamos definir duas correntes em cada malha, vamos denominá-las de i   e   i 2 . Agora, nós podemos fazer análise das malhas.

Malha 1: 36 e - 3 t - 6 i - v = 0

Malha 2:   v - 12 i 2 = 0

Belezinha, pessoal. Agora que já sabemos as equações, vamos pegá-las para formar um sistema de equações e acharmos a EDO do circuito.

36 e - 3 t - 6 i - v = 0       ⋅ ( - 2 )

v - 12 i 2 = 0

- 72 e - 3 t + 12 i + 2 v = 0   +

v - 12 i 2 = 0

- 72 e - 3 t + 12 i + 3 v - 12 i 2 = 0

12 i - i 2 + 3 v - 7 2 e - 3 t = 0

Vamos denominar o i - i 2 como i c .

12 i c + 3 v = 72 e - 3 t

E chegamos na EDO! Agora, vamos resolver juntinhos 😉

Passo 2

Muito bom! Resolvendo a EDO, iremos encontrar nosso v ( t ) . Vamos lá, pessoal!

12 ⋅ C ⋅ d v d t = 72 e - 3 t - 3 v

12 ⋅ 1 8 ⋅ d v d t = 72 e - 3 t - 3 v

d v 72 e - 3 t - 3 v = 8 12 ⋅ d t

d v 72 e - 3 t - 3 v = 2 3 ⋅ d t

Putz! E agora??? 😲 Ixiii...vamos ter que usar integral. Mas, fica tranquilo, vamos te mostrar como é de boa. Partiu?

∫ d v 72 e - 3 t - 3 v  

Vamos substituir 72 e - 3 t - 3 v = u e d u = - 3 d v

∫ d v 72 e - 3 t - 3 v   = - 1 3 ∫ d u u  

- 1 3 ∫ d u u   = - 1 3 l n ⁡ ( 72 e - 3 t - 3 v )

- 1 3 ln ⁡ 72 e - 3 t - 3 v = 2 3 t

- ln ⁡ 72 e - 3 t - 3 v = 2 t + C

ln ⁡ 72 e - 3 t - 3 v = - 2 t + C

72 e - 3 t - 3 v = e - 2 t ⋅ C

v = - C ⋅ e - 2 t + 72 e - 3 t 3

v = - C + 24 e - 3 t

Passo 3

Ufaaa! Finalmente, achamos nossa expressão para o v , mas peraí, não sabemos quanto vale a constante C. Para isso, vamos pegar a expressão que descobrimos e usar o v = - 6 .

- 6 = - C + 24 e - 3 t

C = 24 e - 3 t + 6

Belezinha, pessoal. Essa parte foi bem tranquila né? Ei, estamos quase terminando, só vamos achar agora o v ( t ) e o i t . Para o v ( t ) vamos usar: v ( t ) = - ( 24 e - 3 t + 6 ) ⋅ e - 2 t + 24

Blz! Vamos substituir os valores que já temos

v t = - 24 e - 6 t + 6 e - 3 t + 24 V

Muito bem! Agora, lembra da nossa análise da primeira malha??? Vamos usá-la novamente e, assim, acharemos a corrente.

36 - 6 i - v = 0

36 - 6 i - 24 e - 6 t + 6 e - 3 t + 24 = 0

i = - 4 e - 6 t + 6 e - 3 t + 10 A

Resposta

v t = - 24 e - 6 t + 6 e - 3 t + 24 V

i ( t ) = - 4 e - 6 t + 6 e - 3 t + 10 A

Exercícios de Livros Relacionados

A Figura 7.146 mostra um circuito para estabelecer o período em que é aplicada tensão aos eletrodos de uma máquina de soldar. O tempo é contabilizado em termos de quanto tempo leva para o capacitor se
O circuito na Figura 7.148a pode ser projetado como um integrador ou diferenciador aproximado, dependendo se a saída for em cima do resistor ou do capacitor, bem como da constante de tempo τ=R C do ci
Uma ponta de prova de atenuação empregada em osciloscópios foi projetada para reduzir a magnitude da tensão de entrada vi por um fator 10. Conforme ilustrado na Figura 7.149, o osciloscópio possui res
Para movimentar um ponto na tela de um tubo de raios catódicos, é necessário um aumento linear na tensão nas placas de deflexão, conforme mostrado na Figura 7.151. Dado que a capacitância das placas é
No circuito da figura 7.79, a tensão no capacitor imediatamente antes de t = 0 é: a10 V b 7 V c6 V d4 V e0 V