Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 39

Repita o Prob. 13.38 para o sistema do Prob. 13.27.

Passo 1

Vamos para a penúltima questão!! Vc já deve estar beeeem fera em resolver essas questões viu?

Mas enfim... Pelo enunciado, temos o seguinte circuito:

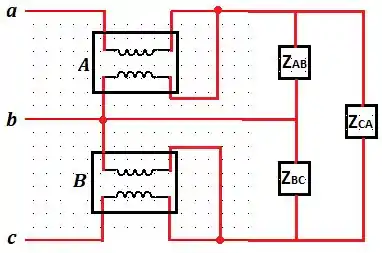
Em que Z A B , Z B C e Z C A valem, respectivamente, j 1 0   Ω , 20   Ω e - j 10   Ω . Além disso, V a b = 1 00 3 ∠ 3 0 °   V (já fazendo a relação entre tensão de linha e de fase).

Passo 2

Dessa forma, podemos calcular as correntes de fase da seguinte forma:

I A B = V A B Z A B = 100 3 ∠ 30 °   j 10 = 10 3 ∠ - 6 0 °   A

I B C = V B C Z B C = 100 3 ∠ - 9 0 °   20 = 5 3 ∠ - 90 °   A

I C A = V C A Z C A = 100 3 ∠ 15 0 °   - j 10 = 10 3 ∠ 24 0 °   A

E, pela Lei dos Nós, temos que as correntes de linha são dadas por:

I a = I A B - I C A = 10 3 ∠ - 60 ° - 10 3 ∠ 240 ° = 10 3 ∠ 0 °   A

I c = I C A - I B C = 10 3 ∠ 240 ° - 5 3 ∠ - 90 ° = 10.7 3 ∠ - 143.8 °   A

Passo 3

Analisando a figura, temos que as tensões são:

V a b = 1 00 3 ∠ 3 0 °   V

V c b = - V b c = 100 3 ∠ 9 0 °   V

Passo 4

Nesse sentido, a leitura que o wattímetro A está lendo é dada por:

P A = V a b I a cos ⁡ θ V a b - θ I a ∴

P A = 100 3 × 10 3 cos ⁡ 3 0 ° - 0 ° ∴

P A = 15 00 3   W

Ainda, a leitura que o wattímetro B está lendo é dada por:

P B = V c b I c cos ⁡ θ V c b - θ c ∴

P B = 100 3 × 10.7 3 cos ⁡ 9 0 ° - ( - 143.8 ° ) ∴

P B = - 1097.6   W

Logo, somando as duas potências, temos que a potência total fornecida às cargas é:

P = P A + P B ≈ 1.5   k W

Agora pra finalizar vamos para a última questão desse capítulo!! (Ufaaaaa)

Resposta

P =   1.5   k W