Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.1 - Ex. 2
No sistema equilibrado, a carga consome , com fator de potência 0,8 atrasado. Capacitores sáo conectados a cada fase da carga, para aumentar seu fator de potência para 0,9 atrasado. Calcule o valor de capacitância necessário, com uma frequência de e tensōes de linha de (eficazes).
Passo 1
E aí gurizada tudo belezinha? O enunciado pede que a gente determine o valor de capacitância necessário, com uma frequência de e tensōes de linha de (eficazes), os dados do enunciado são:
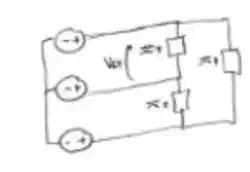
Esboçando o circuito temos:
var
Passo 2
Resposta
Exercícios de Livros Relacionados
A potência total medida em um sistema trifásico que alimenta uma carga conectada em estrela equilibrada é de 12 kW com fator de potência 0,6 (adiantado). Se a tensão de linha for 208 V, calcule a corr
Uma linha trifásica tem impedância de 1 + j3 Ω por fase. A linha alimenta uma carga conectada em triângulo equilibrada que absorve uma potência complexa total de 12 + j5 kVA. Se a tensão de linha no l
Uma fonte conectada em estrela equilibrada e de sequência positiva tem V a n = 240 0 V RMS e alimenta uma carga conectada em triângulo desequilibrada por meio de uma linha de transmissão de impedância
Determine a potência real absorvida pela carga na Figura 12.58.
A fonte da Figura 12.65 está equilibrada e apresenta uma sequência de fases positiva. Se f=60H z , use o PSpice ou MultiSim para determinar V A N ,V B NeV C N .