Sketch the resistor voltage in a simple RL circuit characterized by an initial energy of 15 mJ stored in the 10 mH inductor for R = 1 kΩ, R = 10 kΩ, and R = 100kΩ. Verify your solution with a single PSpice simulation.
Passo 1
Fala, galera!! Primeiramente vamos montar a expressão que representa o comportamento da corrente do indutor e depois variaremos os valores de R. Como temos a energia inicial armazenada, podemos encontrar a corrente inicial no indutor:
Portanto nossa expressão será:
Para R = 1 kΩ:
Para R = 10 kΩ:
Para R = 100 kΩ:
Passo 2
O livro pede que se use o PSpice para fazer a simulação das curvas, mas na prática podemos usar outros simuladores. Como você também pode usar o de sua preferência. Aqui utilizaremos o MultiSim:
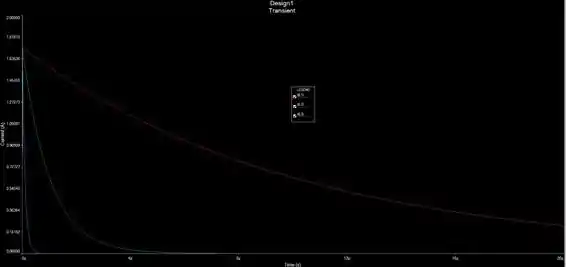
Como podemos ver, as curvas realmente seguiram o comportamento esperado. A curva vermelha (para o R = 1 kΩ), possui um decaimento mais suave, devido a resistência mais baixa e por consequência constante de tempo mais alta. A curva verde (para R = 10 kΩ) já nos mostra um comportamento mais acentuado do que o da curva vermelha devido a resistência mais alta e a constante de tempo mais baixa. E por fim, a curva azul (Para R = 100 kΩ) possui o decaimento mais rápido de todos, devido a sua alta resistência e, consequentemente, e baixa constante de tempo
Portanto, as curvas do gráfico batem com o comportamento esperado para as expressões encontradas. E assim finalizamos mais uma, famlilia!
Resposta
Para R = 1 kΩ:
Para R = 10 kΩ:
Para R = 100 kΩ: