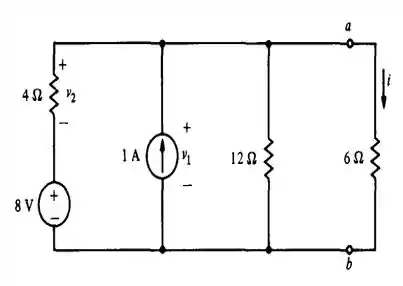
Substitua tudo no circuito do Ex. 5.3.1, exceto a fonte de 1 A, pelo seu circuito equivalente de Thevenin e use o resultado para calcular .
Passo 1
E aí, galerinha! Tudo tranks? Simbora pra mais uma questãozinha aí!?
Bom! Precisamos encontrar o circuito equivalente de Thévenin para o circuito como no esquema abaixo, onde é a fonte de tensão que passa ali onde circula a corrente de ...
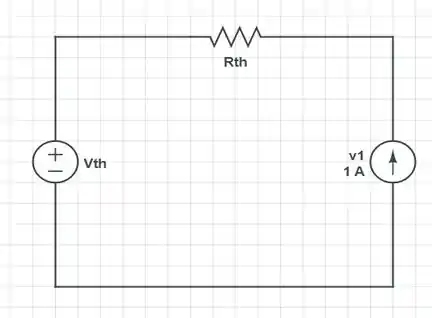
Passo 2
Para encontrar a resistência de Thévenin, vamos começar excluindo todas as fontes independentes desse circuito...
Com isso, ficamos com aquelas três resistências de , e em paralelo... Sendo assim;
Passo 3
Para achar então, vamos então recorrer ao método do divisor de tensão... Aquelas duas resistências de e estão em paralelo.
Isso nos dá que o circuito pode ser reescrito como...

Então, pra achar basta usar o método do divisor de tensão...
Passo 4
Finalmente, pra achar basta aplicar a análise de malhas...
Como :
Pronto! Sucesso, guys! Missão cumprida!