Suponha que o circuito analisado no Problema seja parte de um filtro Butterworth passa-baixas de terceira ordem com um ganho na faixa de passagem de 8 .
a) Se F na parte do filtro que corresponde à seçāo de segunda ordem, qual é o limite superior para ?b) Se for escolhido o valor limite de , quais serão os valores prototípicos de e ?c) Se a frequência de corte do filtro for e se for escolhido o valor de para , calcule os novos valores de e .d) Especifique os novos valores dos resistores e do capacitor na seção de primeira ordem do filtro.e) Faça o diagrama do circuito e identifique todos os valores de componentes no diagrama.
Passo 1
E aí gurizada tudo belezinha? O enunciado pede que a gente determine a) Se F na parte do filtro que corresponde à seçāo de segunda ordem, qual é o limite superior para ?
Passo 2
b) Se for escolhido o valor limite de , quais serão os valores prototípicos de e ?
[b] ;
Passo 3
c) Se a frequência de corte do filtro for e se for escolhido o valor de para , calcule os novos valores de e .
[c] ;
Passo 4
d) Especifique os novos valores dos resistores e do capacitor na seção de primeira ordem do filtro.
Passo 5
e) Faça o diagrama do circuito e identifique todos os valores de componentes no diagrama.
e- Por hipótese, o circuito se torna:
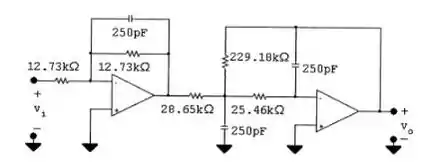
Resposta
a.
b.
c.
d.