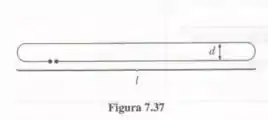
Tente calcular a auto indutância da espira em forma de 'grampo de cabelo' mostrada na Figura 7.37. (Despreze a contribuição das extremidades; a maior parte do fluxo vem da parte longa e reta.) Você vai se deparar com um problema que é característico de muitos cálculos de auto indutância. Para obter uma resposta definitiva, assuma que o fio tem um raio minúsculo, e ignore qualquer fluxo que passa pelo fio em si.

Olá pessoal, bora para mais uma!?

O campo do fio é dado por:

Com isso o fluxo é dado por:

Ressaltando que no numerador é desprezível quando comparado a d, mas no denominador não podemos ter se não o fluxo é infinito.