- Usando a abordagem do supernó, determine as tensões nodais para os circuitos vistos na Figura 8.117.
- Determine a tensão entre os terminais de todas as fontes de corrente.
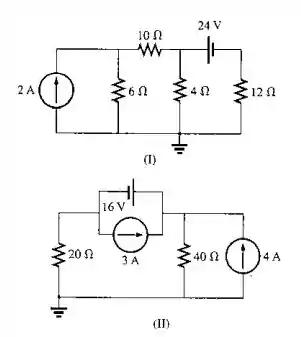
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
- Vamos redesenhar o circuito elétrico, como mostrado na figura a seguir, vulgo figura (1) rs, show?
- Vamos redesenhar a rede do circuito elétrico como mostrado na figura a seguir, vulgo figura 2, ne ? Show kk
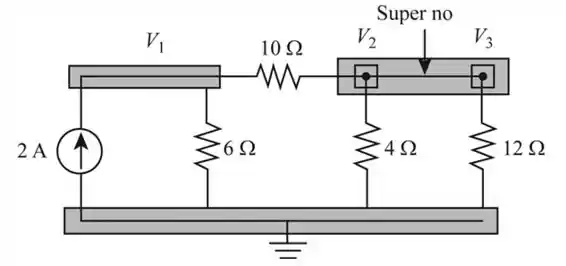
Passo 2
Vamos aplicar a lei de Kirchhoff no supernó 1
Vamos aplicar a lei de Kirchhoff no supernó 2 e 3
Consideraremos a fonte independente na Figura 1, e iremos encontrar a tensão usando a abordagem de supernó
Passo 3
Substituindo a expressão (3) na expressão (2)
Com base na equação (1) e a equação (4), iremos calcular os valores de tensão
Podemos utilizar alguns métodos, porém para iremos utilizar a regra de cramer, para melhor visualização
Vamos calcular o determinante da matriz
Agora para encontrarmos o determinante de vamos substituir as linhas pós o sinal de igual.
Agora para encontrarmos o determinante de vamos substituir as linhas pós o sinal de igual.
Temos que
Substituindo os valores temos
Pronto, conseguimos encontrar
Vamos substituir na equação (3)
Logo, os valores de tensão são , respectivamente.
Passo 4
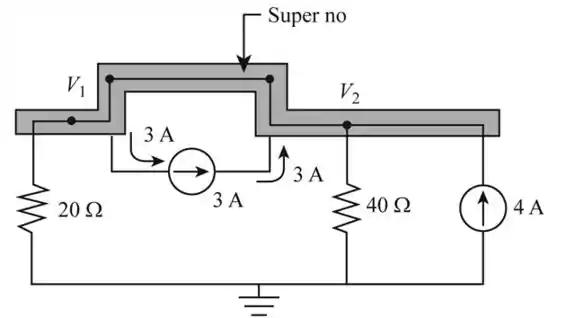
Passo 2
Vamos considerar o super nó da Figura 2, e iremos encontrar a tensão usando a abordagem de super-nó.
Considerando a fonte independente na Figura 2, iremos encontrar a tensão usando a abordagem do super nó
Substituindo a equação (6) na equação (5), temos
Logo, os valores de tensão são , respectivamente.
Resposta
- Logo, os valores de tensão são , respectivamente.
- Logo, os valores de tensão são , respectivamente.