Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 15.Problemas - Ex. 28
a) Usando capacitores de 50 nF, projete um
filtro ativo passa-faixa de banda larga de
primeira ordem que tenha uma frequência
de corte inferior de 200 Hz, uma frequên-
cia de corte superior de 2.000 Hz e um
ganho na faixa de passagem de 20 dB. Use
filtros protótipos passa-baixas e passa-altas
no projeto (veja os problemas 15.26 e
15.27).
b) Escreva a função de transferência do fil-
tro modificado.
c) Use a função de transferência do item (b)
para determinar H(jvo), onde vo é a fre-
quência central do filtro.
d) Qual é o ganho (em decibéis) da faixa de
passagem do filtro em vo?
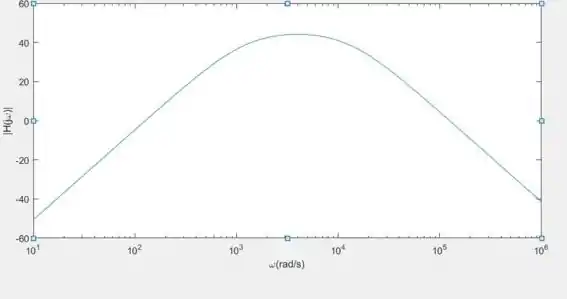
e) Usando um programa de computador de
sua escolha, construa um diagrama de
Bode de amplitude do filtro.
Passo 1
- A função de transferência sem escala Hhp do filtro passa-altas é dada por,
- Determine a função de transferência do circuito H'(s),
- Determine a frequência central do filtro ,
- Determine o ganho de banda passante do filtro G em ,
Determinar o fator de escala de frequência,
onde é dada a frequência de corte mais baixa.
então, a função de transferência escalonada do filtro passa-alta é dada por
Determine a entrada do filtro passa-alta e os resistores de realimentação,
onde é o tamanho do capacitor dado.
A função de transferência sem escala Hp do filtro passa-baixa é dada por,
Determine o fator de escala de frequência ,
onde é dada a frequência de corte superior.
Então, a função de transferência escalonada do filtro passa-baixa é dada por,
Determine a entrada do filtro passa-baixa e os resistores de realimentação RL
Onde é o tamanho do capacitor fornecido.
Seja a resistência de entrada R do amplificador inversor como segue,
Determine o resistor de realimentação do amplificador inversor
Passo 2
Substitua na função de transferência H'(s),
Passo 3
Resposta
- Ver a figura