a) Use os circuitos analisados nos problemas e para implementar um filtro rejeita-faixa de banda larga que tenha um ganho na faixa de passagem de , uma freqüência de corte inferior de , uma freqüência de corte superior de e uma atenuaçāo de, no mínimo, em e em . Use capacitores de sempre que possivel.b) Desenhe o diagrama do circuito e identifique todos os componentes.

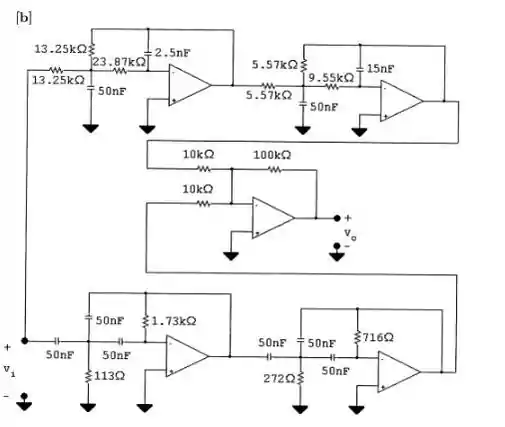
[a] Filtro passa-baixa com ganho de 0" " dB (manuseie o ganho de banda passante de 20" " dB em uma seção de ganho separada):

Na primeira seção de segunda ordem do protótipo:

escolha

Selecione arbitrariamente o valor maior para e, em seguida,

Portanto, no primeiro circuito protótipo de segunda ordem

No circuito protótipo de segunda ordem:

escolha

Selecione arbitrariamente o valor maior e, em seguida,

Na seção passa-baixa do filtro

Portanto, na primeira seção de segunda ordem em escala

Na segunda seção de segunda ordem dimensionada

Seção de filtro passa-alta com ganho de 0 dB (lidar com ganho de banda passante de 20 dB em uma seção de ganho separada):

Na primeira seção de segunda ordem do protótipo:

Na seção do segundo protótipo de segunda ordem:

Na seção passa-alta do filtro

Na primeira seção de segunda ordem em escala

Na segunda seção de segunda ordem dimensionada

Na seção de ganho, deixe