Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.Problemas - Ex. 26a

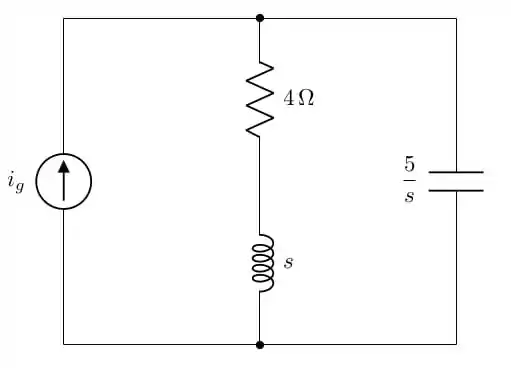
Use a equação representativa e transformadas de Laplace para calcular v , para t > 0 , se

a )   i g = 2 u t   A

Passo 1

E aí, moçada. Vamos começar nossa jornada resolvendo circuitos usando transformadas ao invés de equações características.

Como o circuito não está chaveado e não foram dadas condições iniciais, tudo o que temos que fazer com o circuito é colocá-lo no domínio da frequência:

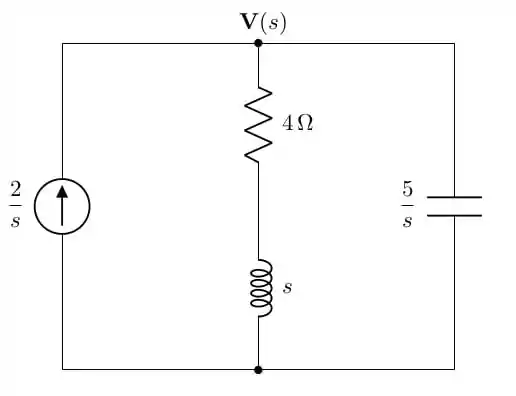
Passo 2

Fazendo a análise de nós do circuito transformado, temos:

V ( s ) 4 + s + V ( s ) 5 / s = 2 s   ⇒ V ( s ) 4 + s + s V ( s ) 5 = 2 s

5 s V s + s 2 4 + s V s 4 + s ⋅ 5 s = 2 ⋅ 5 ⋅ 4 + s 4 + s ⋅ 5 s ⇒ 5 s + 4 s 2 + s 3 V s = 40 + 10 s

V s = 10 s + 40 s ( s 2 + 4 s + 5 ) = 10 s + 40 s ( s + 1 ) ( s + 5 ) = A s + B s + 1 + C s + 5

Passo 3

O próximo passo é calcular os coeficientes das frações parciais:

A = s V s s = 0 = 10 s + 40 s + 1 s + 5 s = 0 = 40 1 ⋅ 5 ⇒ A = 8

B = ( s + 1 ) V s s = - 1 = 10 s + 40 s ⋅ s + 5 s = - 1 = 10 - 1 + 40 - 1 ( - 1 + 5 ) = 30 - 4 ⇒ B = - 15 2

C = ( s + 5 ) V s s = - 5 = 10 s + 40 s ⋅ s + 1 s = - 5 = 10 - 5 + 40 - 5 ( - 5 + 1 ) = - 10 20 ⇒ C = - 1 2

Assim, a expressão para V ( s ) que é a mesma para a tensão em cima do capacitor é:

V s = 8 s - 15 2 ⋅ 1 s + 1 - 1 2 ⋅ 1 s + 5

Com isso, a expressão para a tensão em cima do capacitor será:

v t = 8 - 15 2 e - t - 1 2 e - 5 t u ( t )

Resposta

v t = 8 - 15 2 e - t - 1 2 e - 5 t u ( t )