Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.Problemas - Ex. 29

Use a equação representativa e transformadas de Laplace para calcular i , para t > 0 , se i 0 = 2   A e v 0 = 6   V .

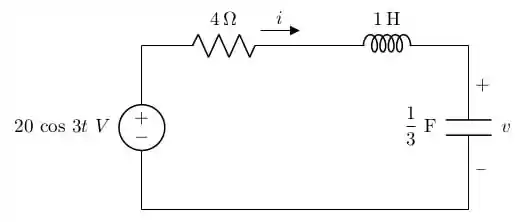
Passo 1

Uhuuuuuu! Vamos comemorar! Não teremos que calcular as condições iniciais nem nos preocuparmos com chaveamento. Então, vamos partir logo para o circuito transformado e fazer a análise de circuitos.

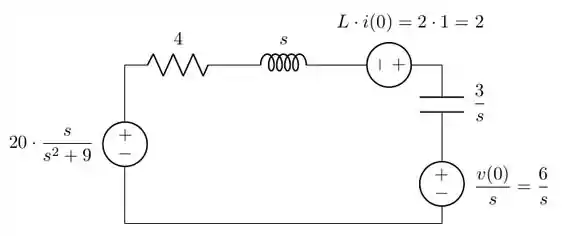
Passo 2

Como o circuito possui apenas uma malha, podemos calcular a corrente que circula nele usando a lei de Ohm:

I s = ∑ V ( s ) ∑ Z ( s ) = ∑ V ( s ) ⋅ ∑ Z s - 1 = 20 s s 2 + 9 + 2 - 6 s ⋅ 4 + s + 3 s - 1

= 20 s ⋅ s + 2 s s 2 + 9 - 6 ( s 2 + 9 ) s ( s 2 + 9 ) ⋅ 4 s + s 2 + 3 s - 1

= 20 s 2 + 2 s 3 + 18 s - 6 s 2 - 54 s ( s 2 + 9 ) ⋅ s s 2 + 4 s + 3

I s = 2 s 3 + 14 s 2 + 18 s - 54 ( s 2 + 9 ) ( s + 1 ) ( s + 3 )

Passo 3

Neste ponto, vamos fazer o que fizemos na questão anterior: vamos usar o matlab para calcular as frações parciais e já nos fornecer a resposta com apenas algumas linhas de código:

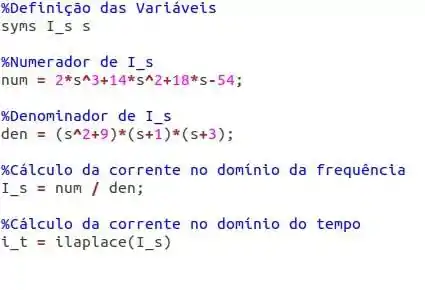
Para chamar a função, basta digitar no console o nome da função com a extensão .m. No nosso caso, escolhemos cap18_29.m. Ao digitar isso no console, obtemos a resposta:

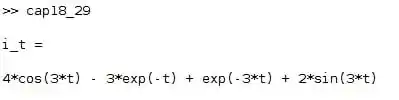
Assim, a corrente no domínio do tempo é:

i t = 4 cos ⁡ 3 t - 3 e - t + e - 3 t + 2 sin ⁡ 3 t u ( t )

Espero ter te convencido que os problemas de engenharia são facilmente resolvidos com o auxílio de programas computacionais e que essa é a rotina de um engenheiro. Percebam que nem precisamos ficar de lenga-lenga calculando frações parciais ou transformadas inversas. Então, Partiu resolver mais questões.

Resposta

i t = 4 cos ⁡ 3 t - 3 e - t + e - 3 t + 2 sin ⁡ 3 t u ( t )