Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 18.Problemas - Ex. 28
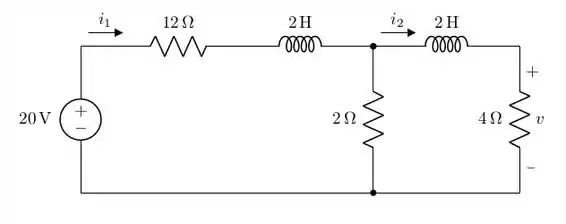
Use a equação representativa e transformadas de Laplace para calcular , para , se e
Passo 1
Uhuuuuuu! Vamos comemorar! Não teremos que calcular as condições iniciais nem nos preocuparmos com chaveamento. Então, vamos partir logo para o circuito transformado e fazer a análise de circuitos.
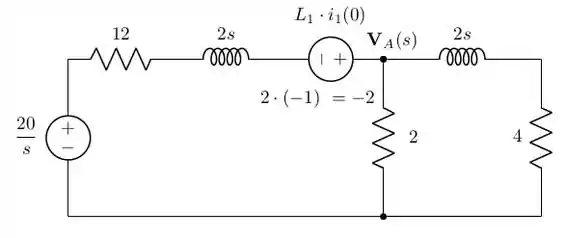
Vamos começar usando a análise de nós:
Passo 2
Neste ponto, vamos fazer algo diferente. A análise de circuitos foi feita. Vamos profissionalizar nossa resposta e torná-la mais próxima da engenharia. Vamos resolver a equação computacionalmente. Para isso, vamos fazer um pequeno script no matlab e ver o quanto nós economizamos de tempo na resolução “na prática”:
O script em questão é este:
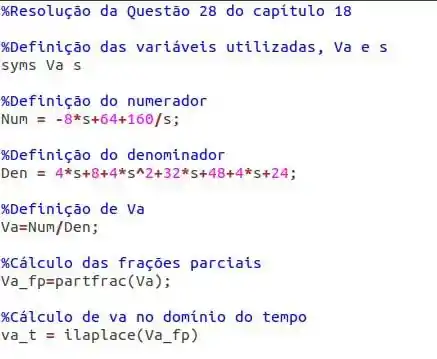
Salvaremos com o nome que quisermos, mas devemos nos lembrar de nomeá-lo com uma extensão .m. Depois, é só digitar o nome que salvamos no console e o matlab nos dará a resposta. No nosso caso, o arquivo salvo foi nomeado de “cap18_28.m”. Assim:
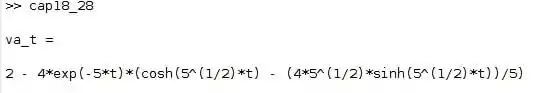
Logo, nossa resposta será
Viu, com algumas linhas de código conseguimos reduzir nosso problema significativamente. Vamos usar este método novamente na próxima questão para ver se você fixou o problema.