Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.Problemas - Ex. 7

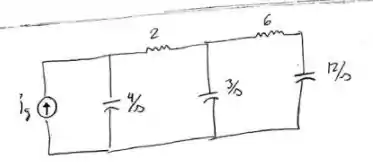
Use o método do Prob. 14.6 para calcular a impedância vista da fonte. e use o resultado para calcular a resposta forçada t

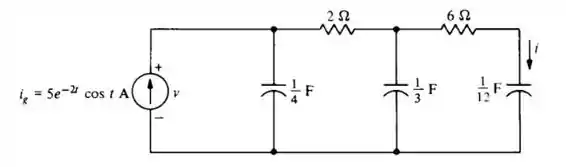
Passo 1

O enunciado pede que a gente calcule a impedância vista da fonte. e use o resultado para calcular a resposta forçada t . Então vamos representar o circuito , vem comigo :)

i g = 5 R - 2 t c o s ⁡ A

s = - 2 + j                   I ( s ) = 5 ∠ 0 ∘

z ' = 6 + ( - 2 + j ) 12 = 5,834 ∠ 0 , 82 ∘

y ' ' = ( - 2 + j ) 3 + 1 5,834 < 0,82 = 0,6 < 146,25 °

z ' ' ' = 2 + 1 y ' ' = 1,111 L - 56 , 44 ∘

y e q   = ( - 2 + j ) 4 + 1 1,11 L - 56 , { 4 = 1 < 90 ∘

V s = i g ⋅ 1 Y e q = 5 1 < 90 ° = 5 < - 90 ∘

V ( f ) = 5 e - 2 t s e n ⁡ t A

Resposta

V ( f ) = 5 e - 2 t s e n ⁡ t A

Exercícios de Livros Relacionados

Mostre que, para a figura do Problema 15.4 H s = V 3 ( s ) V 1 ( s ) = - 1 R 1 s 2 + 1 R 2 s + 1 R 3 Escolha valores para as resistências de forma que o circuito seja um filtro passa-baixas butterwort
Se o ganho de um filtro passa-baixas com função de rede H ( s ) e definido como K = | H ( 0 ) | , compare os ganhos nos casos gerais dos Problemas 15.13 e 15.19, que são, respectivamente, circuitos pa
Usando o resultado do Problema 15.10, obtenha um filtro passa-faixa tendo a forma da figura do Problema 15.4, com w 0 = 1 r a d s ,Q = 10eG = 2 . Calcule os pontos de corte aproximados e a largura da
Mostre calculando V 2 V 1 que o circuito é um filtro passa-faixa e calcule o ganho, a largura da faixa e a frequência central.
Uma carga equilibrada, ligada em Y, tem uma impedância de 60 - j45 Ω / ϕ e está ligada emparalelo com uma carga equilibrada, ligada em ∆ , cuja impedância é 90 2 / 45 °Ω / ϕ . Ascargas em paralelo são